Unité

[Rockleader]

Bonjour, j'aimerais connaître les unités de chacun des termes suivant, le seul que je connaisse soit Lambda qui n'a pas d'unité =)





Egalement:



A représente l'activité d'un échantillon radioactif, c'est en Bq. Lambda n'ayant pas de dimension, il ne reste que N le nombre de noyau radioactif: est ce que N a une unité préscise ?

[Rockleader]

Si quelqun avait une réponse claire, merci c'est assez urgent...demain matin 8h30...

[manoa]

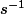
pour c'est , ... vu que =1/to et (to) a une dimension temporelle.
Pas d'unité pour N.

[Skullkid]

D'une façon générale, en physique, les fonctions exp, sin, cos et ln ne mangent que des nombres sans dimension. Si tu as exp(ab) dans une formule, ab est forcément sans dimension. Donc si a est en mètres, b est forcément en 1/mètres.

[Rockleader]

Merci beaucoup à vous deux !!!

[Mathusalem]

C'est un peu un argument peu concret, mais tu peux aussi voir la chose ainsi :

Si tu as des mètres désignés par une variable x qui passe dans une fonction x^2, tu te retrouves avec des mètres au carré.

Ces mètres au carré peuvent signifier que tu parles d'une surface (un concept bien acquis). Mais ils peuvent aussi signifier simplement qu'une certaine distance intervient de manière compliquée dans un concept physique. Par exemple, la force d'un ressort, c'est -kx où x est une distance d'élongation. Quand t'en veux le potentiel, tu dois en calculer le travail, et tu te retrouves avec du x^2 (donc des m^2 ou des mm^2 ou des cms^2 etc..) mais en soit ce n'est pas une aire, même si c'en a les unités.

Tu dois maintenant te poser la question : si je prends des mètres et que je les passe à une fonction ln par exemple, que représente cette dimension ln[m] ? ou que représentrait une dimension e^[m] ?