Le tir de précision

[Lacryzz]

Bonjour j'ai un DM de physique a faire pour mercredi et je bloque sur certaines questions.

On considérera que le référentiel terrestre peut être assimilé a un référentiel galiléen, et on négligera les frottements dans l'air.
Un tireur d'élite est posté sur le toit d'un bâtiment de hauteur h. Il vise une cible se trouvant au niveau du sol à une distance d. Son fusil lance des projectiles de masse m, qui sortent du canon a une vitesse v0.
Le repère sera choisi de telle sorte que l'origine est au niveau du sol, a la meme abscisse que le tireur ( je ne vois pas comment le représenter). L'axe des abscisses (Ox) est orienté dans la direction du tir vers la cible ; l'axe des altitudes (Oz est orienté vers le haut.
On appelle alpha l'angle entre le vecteur vitesse initiale v0 et l'horizontale, comté positivement dans le sens trigonométrique. Ainsi, alpha >0 correspond a un tir vers le haut et alpha <0 à un tir vers le bas.

1)a. Exprimer les coordonnées du point de départ A de la balle , et celles de la cible B
b. Faire l'inventaire des forces s'exerçant sur la balle une fois sortie du canon du fusil, en déduire son accélération (vecteur) a
c. Déduire de tout cela les lois horaires du mouvement de la balle
d. Etablir l'équation de la trajectoire de la balle. De quelle nature est cette trajectoire ?
e. Faire un schéma où figureront les axes, A et B, l'angle alpha et y dessiner la trajectoire de la balle

2) Pour atteindre sa cible, le tireur doit ajuster l'angle. On cherche à savoir comment il fait s'y prendre quand le fusil est muni d'une lunette de visée dont l'ace est parallèle à celui du canon.
a. Déterminer l'angle alpha (0) lorsque le tireur a sa cible exactement au centre du réticule (croix centrée dans le champ du viseur).

b. Déterminer les temps t1 que mettrait la balle pour aller du tireur à sa cible, en ligne droite, à la vitesse v0.

c. On suppose que le temps mis par la balle à atteindre la cible est pratiquement égal à t1
Calculer la déviation verticale delta z0 de la balle par rapport à la ligne droite.

J'ai fait toute la question 1 mais je bloque a partir de la 2. Si vous pouviez m'aidez je vous en serais grandement reconnaissant. En attendant voici ce que j'ai fait aux questions 1c. et 1d.

1)c.
On a après avoir dérivé :
vx = v0 cos alpha
vz = -gt + v0 sin alpha
On en déduit la loi horaire :
x = v0 t cos alpha
z = -1/2g t (carré) + v0 sin alpha

1)d.
On a : t =x/v0 cos alpha
d'où,
z = -1/2 gt (carré) + v0 sin alpha
et en remplaçant par t, on obtient :
z = -gx (carré) /2v0 (carré) cos (carré) alpha + xtan alpha

Merci pour votre aide
Lacryzz
P-S : je n'ai pas trouvé comment écrire les exposants et les indices, donc désolé si c'est peu pratique a lire.

[Sake]

Salut,

Tu n'as pas répondu aux questions 1)a) et 1)b). Est-ce l'énoncé qui cause problème? Je comprends à la limite pourquoi: Il est assez mal formulé. Mais les notions d'abscisse et d'ordonnée ne devraient pas te poser trop de soucis.

[Lacryzz]

J’ai répondu aux questions a et b :
1a. Les coordonnées sont :
A (0,h) et B ( racine(d^2 - h^2),0)

1b. Il y a une seule force qui est le poids de formule
P= mg (avec les vecteurs bien sûr)
D’apres la deuxième loi de Newton, on a :
ma = P (a étant l’accélération)
ma=mg
a=g

[Sake]

Ah, c'est bien. Je pensais que tu avais bloqué à la question 1)a) car tu avais écrit :

Le repère sera choisi de telle sorte que l'origine est au niveau du sol, a la meme abscisse que le tireur ( je ne vois pas comment le représenter).

C'est bon pour les questions 1)a) et 1)b) mais pour la question 1)c) tu t'es trompé. On doit intégrer deux fois par rapport au temps pour obtenir les é̶q̶u̶a̶t̶i̶o̶n̶s̶ ̶d̶u̶ ̶m̶o̶u̶v̶e̶m̶e̶n̶t̶, pas dériver. Malgré tout, tu as fait le bon calcul.

Attention néanmoins pour la loi horaire de z, car tu as oublié d'appliquer la condition initiale.

EDIT: purée je suis pas réveillé ajd. On n'appelle pas ça les équations du mouvement, mais les lois horaires... Ici, l'équation du mouvement est ton PFD (a = dv/dt = g après projection dans l'axe vertical) et les solutions x(t) et z(t) sont les lois horaires.

[Lacryzz]

Mais pourquoi je dois intégrer deux fois ? Car dans mon cours j’ai la même chose. Parce que j’integre l’accélération pour avoir la vitesse qui intégrée me donne la loi horaire.
Et quelle est cette condition initiale ?
Parce que j’ai demandé à d’autres personnes avant et elles m’ont dit que la 1c était juste.

P-S : dans la 1.c le z est faux (j’ai mal recopié)
z = -1/2 gt (carré) + v0 t sin alpha

[Sake]

selon l'axe vertical:


où g est un scalaire.

En intégrant une fois par rapport au temps:

où satisfait la relation . Tu as remarqué en considérant la condition initiale que n'est autre que , d'où .

Maintenant, en intégrant une deuxième fois par rapport au temps, quelle relation obtiens-tu pour ?

[Lacryzz]

Alors en considérant la condition initiale à t= 0, on a z = h et donc on a :
z = -1/2 gt (carré) + v0 t sin alpha + h

[Sake]

Je vois que cette intégration que tu fais est très machinale, voire même recopiée de ce que vous avez fait en cours. Quand on résout une équation différentielle, il est question d'intégrer et on oublie parfois (ce qu'il ne faut absolument pas) qu'intégrer ne se résume pas à trouver une primitive, mais à définir également les bornes d'intégration.

Pour trouver les solutions de l'équation différentielle où est une constante quelconque, on va intégrer à gauche et à droite (entre deux bornes 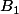et 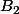à choisir correctement) pour peu que la fonction dispose des bonnes propriétés pour l'intégration au sens de Riemann (ce qu'on suppose a priori pour la plupart des fonctions simples en physique à ton niveau). Cela donne:

, qu'on écrit encore:



On veut bien entendu trouver en tant que solution la fonction évaluée en , donc choisissons . La borne 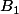peut a priori être arbitraire mais comme l'énoncé nous donnes des indications sur au temps 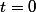(ce qu'on appelle en physique et en maths appliquées une condition initiale, c'est-à-dire une condition aux limites sur la variable temporelle à un instant défini comme étant l'instant initial de l'expérience), on peut en profiter et choisir 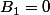car alors est connu. Intégrer à droite ne pose aucun problème car est une constante.

[Sake]

Alors en considérant la condition initiale à t= 0, on a z = h et donc on a :
z = -1/2 gt (carré) + v0 t sin alpha + h

Exactement. Remarque que pour t=0, tu obtiens z(0) = h, ce qui est attendu.

[Lacryzz]

Ok j’ai à peu près compris mais le problème c’est que je n’ai pas encore vu les intégrations en math mais je les comprend. Donc merci.
Est ce que vous pourriez m’aider pour répondre à la question 2 s’il vous plaît ?
J’ai commencé à dire que x=d donc on a :
v0 t cos alpha = d <=> t = d/ v0 cos alpha
Mais après je sais pas s’il fait remplacer t dans z ou alors faire autre chose. J’avais pensé à écrire les lois horaires du mouvement de la cible pour ensuite écrire une égalité entre le z de la balle et le z de la cible et enfin trouver alpha en fonction de h et d.
Après avoir fait les calculs on obtiendrait z’ (pour la cible) qui vaut : z’ = -1/2gt (carré)
Et donc on aurait z = z’
D’où on a aussi t= -h/v0 sin alpha
En égalisant les t on trouve : tan alpha = -h/d ce qui peut être assez logique car alpha est négatif étant donné que c’est un tir vers le bas.
Après cela reste une suggestion qui est peut être loin d’etre la réponse.
Je vous remercie de votre aide future.
Lacryzz

[Sake]

En effet, difficile de comprendre l'intégration quand on n'a pas encore vu ce que c'est.

Qu. 2: N'écrivons pas encore d'équation. Il faut comprendre ce que l'énoncé veut nous demander.
Pour la question 2)a), on te demande quoi?

[Lacryzz]

J’ai en fait trouvé, il faut juste prendre le triangle ABO et écrire alpha en fonction de h et d et j’ai trouvé après calculs : sin alpha = h/d

[Sake]

Oui, c'est ça.

Pour la qu. 2)b) ça doit rouler. Comment tu fais?

[Lacryzz]

v=d/t et donc t= d/v mais après je bloque pour la question 2c.

[Sake]

?

Ce que tu écris serait valide dans le cas où la vitesse est constante dans le temps, sauf qu'ici c'est tout sauf vrai.

A partir des lois du mouvement (x(t) et z(t)), tu as deux façons de trouver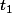 , dont une est selon moi un peu meilleure que l'autre.

[Lacryzz]

Alors là je vois pas du tout

[Sake]

OUBLIE CE QUE J'AI DIT.

Excuse-moi, j'ai mal lu le sujet, qui fait d'abord l'hypothèse d'un mouvement rectiligne et uniforme pour la balle.

Du coup, pour la question c) j'imagine qu'on te demande ce qu'il en serait pour un problème de ballistique dans lequel la trajectoire de la balle n'est pas R&U mais bien parabolique. Encore une fois, je trouve le sujet très mal écrit, bien que ça ne soit pas une excuse pour l'avoir lu de travers.

[Lacryzz]

Donc ce que j’ai fait est bon ?

[Sake]

Donc ce que j’ai fait est bon ?

Oui. La balle parcourt une distance en un temps , à une vitesse constante donc

[Lacryzz]

Par contre j’ai vraiment aucune idée pour la 2c.
A propos de l’ecriture du sujet je suis d’accord avec vous