Merci pour vos réponses,
je vais poster mon énoncé tout à l'heure.
Pour répondre à Dominique, cela veut dire que si je développe ma formule
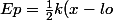^2)
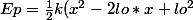)
, je pourrais même dans ce cas supprimer le
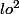
de l'expression de mon énergie, puisque je ne m'intéresse qu'à la variation ?(c'est un exemple, mais donc en général je peux supprimer les termes constants de l'expression d'une énergie ?)
Mais à partir de ce moment là, si j'exprime une autre énergie potentielle, son expression ne sera-t-elle pas faussée ?
Bonjour, dans mes souvenirs de ressort , Ep=Ep elastique+Ep pesanteur, il me vient que souvent on étudiait le mouvement du ressort " horizontale " , et on prennait Ep pesanteur =0 dans ce cas. Si cela peut t'aider.
Merci, justement dans ce cas on travaille sur l'axe horizontal, donc je néglige le travail du poids, et je ne m'occupe pas de l'énergie potentielle de pesanteur.
_________________________________________________
Voilà mon énoncé :
Un point matèriel M de masse m est attaché à deux ressorts horizontaux identiques fixés à deux points fixes A et B.
Constante de raideur des ressorts : k
Longueur à vide des deux ressorts : lo
On prend comme origine le milieu de AB, et quand M est à l'origine (équilibre), la longueur de chaque ressort vaut l1. (AB) est l'axe des abscisses, et x(t) est la position de M à l'instant t.
A t=0, M est abandonné sans vitesse initiale d'une position x0
Le mouvement ayant lieu sans frottement, établir l'équation du mouvement de M par étude énergétique.
Voilà la première question. Je poste ce que j'ai fais dans le post suivant.

 avec x la longueur du ressort et lo sa longueur à vide.
avec x la longueur du ressort et lo sa longueur à vide. (en identifiant avec les Conditions initiales) Or c'est impossible(ca dépend même plus de k... Et au niveau dimensionnel...) Sans la constante ça m'a l'air plus juste.
(en identifiant avec les Conditions initiales) Or c'est impossible(ca dépend même plus de k... Et au niveau dimensionnel...) Sans la constante ça m'a l'air plus juste.