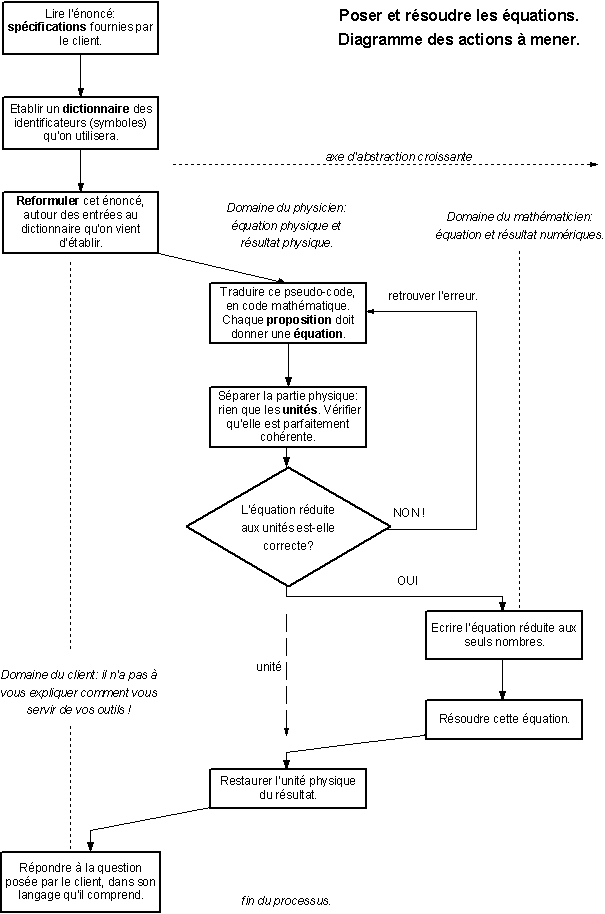
Je constate que c'est presque toujours la panique ici, au moment de comprendre un énoncé, et de le traduire en équations. Voici un guide, en deux étages d'abstraction :
· Première abstraction : du problème formulé par le client, vers une schématisation des phrases d'énoncé en prédicats irréductibles, l'écriture d'un dictionnaire des variables et de leurs symboles (que ce dictionnaire ait une, deux ou dix entrées) et la transcription des prédicats par la pose d'un système d'équations.
· · Seconde abstraction, quand la vérification dimensionnelle est terminée et ne révèle plus d'erreurs, alors résoudre le sous-système numérique, par les méthodes algébriques.
· · Seconde désabstraction : restituer les unités physiques, pour répondre en grandeurs physiques au problème physique.
· Première désabstraction : répondre dans le langage du client, dans des termes qui lui sont accessibles, et qui répondent à son problème.
Un mot est nouveau pour vous : prédicat. C'est une des affirmations fournies par le texte, explicite, ce sera alors grammaticalement une proposition, ou hélas implicite, à chercher plus attentivement, par exemple un adjectif.
Prenons un exemple purement mathématique, qui se présente comme une farce :
"J'ai trois fois l'âge que vous aviez quand j'avais l'âge que vous avez".
Il manque une donnée, que je vous donne : la somme des âges actuels est de 60 ans.
Il faut construire un dictionnaire des variables, qui sont ici au nombre de cinq.
Mon âge actuel : A
Votre âge actuel : B
"quand", le prédicat à dénicher : soit d le décalage en années entre ce temps là et le présent.
Mon âge d'alors : a = A - d
Votre âge d'alors : b = B - d.
On a toutes les variables, il faut encore traduire trois prédicats.
"J'ai trois fois l'âge que vous aviez" : A = 3b
"quand j'avais l'âge que vous avez" : B = a
Et somme de soixante : A + B = 60.
La suite de la résolution est facile par substitutions et isolations, et je vous laisse le faire.
Et en physique ? Une partie des prédicats est fournie par l'énoncé. L'autre partie ce sont les principes et lois applicables.
En mécanique, c'est ultra-simple, il n'y a que trois principes :
Conservation de la quantité de mouvement. Pour la changer, il faut faire quelque chose, appliquer une force.
Conservation du moment angulaire. Pour le changer, il faut faire quelque chose, appliquer un couple de forces, ou un moment de force.
Et l'énergie ? C'est plus délicat. Il a fallu les progrès de l'astronomie pour observer des mouvements sans frottements, on dit des mouvements conservatifs, qui conservent l'énergie mécanique. Cela à partir du début 17e siècle : les quatre satellites médicéens de Jupiter confirment les trois lois de Kepler.
Sur Terre, la conservation de l'énergie mécanique est en pratique impossible à obtenir, mais les problèmes scolaires qu'on vous donne en font l'approximation. En revanche l'énergie totale se conserve, avec la chaleur incluse.
Si, il y a encore un principe caché : on utilise la géométrie que vous avez apprise en classe, et qui est valide pour des objets ni trop gros, ni trop petits, à l'échelle de la main humaine. A l'échelle d'un atome ou plus petit ou plus léger, cette géométrie familière est définitivement invalide (hélas, vos profs ne le savent pas). A l'échelle de la Terre, un triangle équilatéral de 10 000 km de côté peut fort bien être tri-rectangle : trois angles droits.
