Mètre par seconde carrée (m/s²)

[coperniq]

Mètre par seconde carrée (m/s²)

Accélération d'un mobile animé d'un mouvement uniformément varié, dont la vitesse varie, en 1 seconde, de 1 mètre par seconde.

Si j'ai bien compris, si la corps va à 100m/s, à la seconde d"après il va à 101m/s puis à la seconde suivante à 102m/s etc......pour chaque seconde écouler il parcours 1 m de plus que dans la seconde précédente.

Merci.

[Benjamin]

Bonjour,
Oui et non en fait. Il ne faut pas oublier que vitesse et accélération sont avant tout des grandeurs vectorielles. Ainsi, lors d'un mouvement circulaire uniforme, le module de l'accélération est constant, de même que celui de la vitesse. Bien qu'il y ait une accélération, le solide n'accélère pas. L'accélération permet seulement d'imprimer la trajectoire circulaire en changeant la direction du vecteur vitesse.
Ensuite, si tu as une trajectoire rectiligne, et que le vecteur accélération est colinéaire à la trajectoire, alors oui, c'est exactement ce que tu as décrit.
Une chose très importante : il ne faut pas oublier que les vecteurs aussi se dérive dans le temps.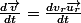 n'est pas égale à 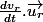mais est égale à .
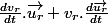Si tu travailles dans la base géocentrique, ou dans le référentiel du labo considéré fixe dans le temps, alors la dérivée de ton vecteur est nulle, et c'est bon. Mais ce n'est pas toujours le cas que tu peux t'affranchir de la dérivation du vecteur. Dans le cas d'un mouvement rectiligne uniforme, suivant l'axe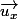 fixe dans le temps, tu auras bien 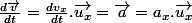et en projetant, tu retombes sur 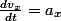, avec dans ton cas 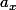constante et donc 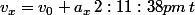. Et alors là, tout se passe comme tu l'as expliqué. Avec 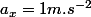, c'est qu'en une seconde, la vitesse augmente de un mètre par seconde... et tu as tout bon

[coperniq]

La définition basique d'une accélération constante, c'est bien:

acceleration = vitesse x temps

Ce qui expliquerai le carré de l'unité de temps (m/s²)

En fait c'est le pourquoi du carré qui m'intriguait, mais maintenant j'ai compris

^^

Donc si je reprend l'acceleration du à la force de pesenteur, elle est constante, elle vaut 9.81

Cela veut il dire qu'à chaque seconde écouler, l'objet va parcourir 9.8m.s ou bien que à chaque fois, il se rebase sur la vitesse acquise l'instant d'avant?

Je crois qu'il serai bon si vous voulez bien de me faire un petit topo sur lé définition de l'acceleration.

Merci.

[Benjamin]

Encore une fois, il ne faut pas faire la confusion entre le vecteur et la norme du vecteur. Tout dépend du repère dans lequel tu travailles après. Un vecteur peut être fixe dans un référentiel et mobile dans un autre. A la base, l'accélération est surtout et avant tout un vecteur.

Pour les définitions :
Tu prends une trajectoire dans un repère de centre O. Tu as un point mobile M(t) sur cette trajectoire.
La définition du vecteur vitesse, c'est : . Autrement dit, pour un (c'est-à-dire un temps) très petit, tu as . En fait, le vecteur vitesse, c'est ce qui va dirigé ton point M selon une direction précise à un instant donné (l'aspect vecteur) tout en lui faisant parcourir une distance dans cette direction dans un certain temps donné (l'aspect norme du vecteur). Elle s'exprime donc en mètre par seconde. En repartant de la formule avec la limite, tu as en fait la définition mathématique de la dérivée et donc .

Ensuite, l'accélération est à la vitesse ce que la vitesse est à la position du point M, tout simplement. Tu as donc (par définition du vecteur accélération) : . Autrement dit, pour un (c'est-à-dire un temps) très petit, tu as . En fait, le vecteur accélération va changer la direction du vecteur vitesse (sauf si les vecteurs accélération et vitesse sont colinéaires à l'instant t), ce qui va alors engendré un changement de trajectoire (aspect vectoriel de l'accélération) tout en changeant la norme du vecteur vitesse (aspect norme du vecteur accélération). Elle s'exprime donc en m/s². En repartant de la formule avec la limite, tu as en fait la définition mathématique de la dérivée et donc .

En résumé, l'aspect vectoriel est indissociable de la définition de l'accélération et de la vitesse. L'accélération définit la trajectoire du fait que c'est un vecteur (dans quel direction est incurvée la trajectoire) et de par sa norme (plus l'accélération est grande, plus la trajectoire est modifiée rapidement et donc plus la courbure est forte). La norme du vecteur vitesse, elle, est directement reliée au temps de parcours.