Bonjour
je tiens à préciser que je ne suis pas celui qui a posté le msg sur les coord. cylindriques.
Comment déterminer le vecteur vitesse en coord. sphériques: Cmt l'exprimer en fonction des 3 vecteurs de base du repérage sphérique??
Merci
Coordonnées sphériques
8 messages
- Page 1 sur 1
Salut,
pour obtenir le vecteur vitesse, il suffit de partir du vecteur position! En effet, il suffit de dériver le vecteur position pour obtenir le vecteur vitesse, et ce, quelle que soit la base choisie.
Ici, si O est l'origine de ton repère, et M le point dont tu veux connaitre la position, tu nommes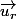 le vecteur radial (le vecteur unité colinéaire à
le vecteur radial (le vecteur unité colinéaire à 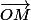 ), et
), et  la distance de M à O,
la distance de M à O,
tu as alors ,
,
donc ,
,
où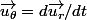 est le vecteur orthoradial.
est le vecteur orthoradial.
Si de plus ( ,
, 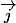 ,
, 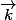 )
)
est une base fixe du référentiel d'étude,
et que) , et
, et ) , où H est le projeté orthogonal de M sur le plan xOy,
, où H est le projeté orthogonal de M sur le plan xOy,
alors les coordonnée x,y,z de M selon ,
, 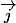 , et
, et 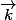 respectivement,
respectivement,
sont ,
,  , et
, et 
pour obtenir le vecteur vitesse, il suffit de partir du vecteur position! En effet, il suffit de dériver le vecteur position pour obtenir le vecteur vitesse, et ce, quelle que soit la base choisie.
Ici, si O est l'origine de ton repère, et M le point dont tu veux connaitre la position, tu nommes
tu as alors
donc
où
Si de plus (
est une base fixe du référentiel d'étude,
et que
alors les coordonnée x,y,z de M selon
sont
dériver
Apartir de cela si tu veux dériver en fonction des coordonnées sphériques comment faire????
La dérive est
r et cos(phi) sont considérer comme des constantes, (téta) est la variable???
d(téta)/d(x) = r*cos (téta)*cos(phi)
Je sais que la vraie réponse est:
d(téta)/d(x) = (cos(téta)*cos(phi))/r
Mais je ne comprends pas?????
La dérive est
r et cos(phi) sont considérer comme des constantes, (téta) est la variable???
d(téta)/d(x) = r*cos (téta)*cos(phi)
Je sais que la vraie réponse est:
d(téta)/d(x) = (cos(téta)*cos(phi))/r
Mais je ne comprends pas?????
Salut!
Pourquoi?
Par ailleurs, par vecteur orthoradial, je comprends: vecteur orthogonal au vecteur radial.. Mais il en existe 1 infinité, non?? Pq affirmer sonunicité. Il manque alors, je pense 1 autre condition ds la définition de ce vecteur.
De même, cmt définir le vecteur u(phi)??
Merci
Alpha a écrit:est le vecteur orthoradial.
Pourquoi?
Par ailleurs, par vecteur orthoradial, je comprends: vecteur orthogonal au vecteur radial.. Mais il en existe 1 infinité, non?? Pq affirmer sonunicité. Il manque alors, je pense 1 autre condition ds la définition de ce vecteur.
De même, cmt définir le vecteur u(phi)??
Merci
En fait, la chose se verrait nettement sur un dessin.
Si tu prends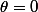 et
et  , ta base de 3 vecteurs
, ta base de 3 vecteurs) coincide avec les vecteurs fixes dans ton référentiel
coincide avec les vecteurs fixes dans ton référentiel ) .
.
En théorie, on pourrait prendre n'importe quel vecteur orhogonal à , pui s on ferait le produit vectoriel de
, pui s on ferait le produit vectoriel de  avec ce dernier vecteur, et ce produit serait égal à un troisième vecteur, et les 3 veteurs ainsi obtenus formeraient une base orthogonale (orthonormale si les vecteurs sont normés).
avec ce dernier vecteur, et ce produit serait égal à un troisième vecteur, et les 3 veteurs ainsi obtenus formeraient une base orthogonale (orthonormale si les vecteurs sont normés).
Dans la pratique, on ne prend pas n'importe quel vecteur orthoradial, c'est pour ça qu'on l'appelle le vecteur orthoradial. Ce vecteur orthoradial pourrait être défini ainsi (modulo manque de rigueur :happy3: ) : c'est le vecteur orthogonal à qui est parallèle au plan formé par les vecteurs
qui est parallèle au plan formé par les vecteurs  et
et 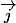 quand
quand  lui est aussi parallèle.
lui est aussi parallèle.
J'essaierai de fournir une meilleure explication si nécessaire.
Si tu prends
En théorie, on pourrait prendre n'importe quel vecteur orhogonal à
Dans la pratique, on ne prend pas n'importe quel vecteur orthoradial, c'est pour ça qu'on l'appelle le vecteur orthoradial. Ce vecteur orthoradial pourrait être défini ainsi (modulo manque de rigueur :happy3: ) : c'est le vecteur orthogonal à
J'essaierai de fournir une meilleure explication si nécessaire.
Voilà, en fait, cela pouvait se dire de manière beaucoup plus simple :
 est unitaire selon
est unitaire selon 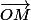
 est est orthogonal à
est est orthogonal à  et se trouve dans le plan zOM,
et se trouve dans le plan zOM,
et
 est orthogonal en M au plan zOM, la base
est orthogonal en M au plan zOM, la base ) étant directe.
étant directe.
(par convention j'appelle le vecteur orthoradial, mais il est vrai que si l'on suit ce que j'avais dit dans mon premier message, on aurait plutôt tendance, "logiquement", à l'appeler
le vecteur orthoradial, mais il est vrai que si l'on suit ce que j'avais dit dans mon premier message, on aurait plutôt tendance, "logiquement", à l'appeler  )
)
En espérant t'avoir apporté quelque éclaircissement.
:happy3:
et
(par convention j'appelle
En espérant t'avoir apporté quelque éclaircissement.
:happy3:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
