Exprimer des coordonnées cylindriques en cartésiennes.

[Jjl]

Bonsoir,j'ai réfléchis sur un exo ou l'on me dit:

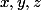
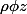
Sachant qu'un point M est défini en coordonnées cartésiennes par M(x,y,z) et en coordonnées cylindrique par ,exprimer en fonction de et inversement,exprimer en fonction de

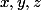
Mais j'ai seulement pu dire que OM(vecteur)== .

Mais pas sûr que ça soit ce qu'on demande.
Un peu d'aide serait la bienvenue.

[WillyCagnes]

bsr

voir ce lien pour t'aider
http://fr.wikipedia.org/wiki/Coordonn%C3%A9es_cylindriques

[Sake]

Bonsoir,j'ai réfléchis sur un exo ou l'on me dit:

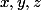
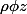
Sachant qu'un point M est défini en coordonnées cartésiennes par M(x,y,z) et en coordonnées cylindrique par ,exprimer en fonction de et inversement,exprimer en fonction de

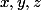
Mais j'ai seulement pu dire que OM(vecteur)== .

Mais pas sûr que ça soit ce qu'on demande.
Un peu d'aide serait la bienvenue.

Salut Jjl,

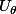
Il faut que tu arrives à exprimer les vecteurs , et en fonction de , ,

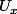
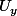
L'un des trois est évident, mais qu'en est-il des deux autres ?

[Jjl]

bsr

voir ce lien pour t'aider
http://fr.wikipedia.org/wiki/Coordonn%C3%A9es_cylindriques

Merci c'est sympa WillyCagnes

[Jjl]

Salut Jjl,

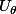
Il faut que tu arrives à exprimer les vecteurs , et en fonction de , ,

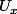
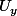
L'un des trois est évident, mais qu'en est-il des deux autres ?

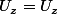
Ah ok,oui donc après je vais réfléchir pour le reste,bien que j'avoue que je ne vois pas trop comment ça va m'aider pour la question. :\