Bonjour,
Voici un DM qui me pose un léger souci.
Déjà le premier exercice:
Deux élèves disposent d'un solénoïde long, de longueur L=60cm, dont ils veulent connaitre le nombre de spires N.
Le comptage des spire une a une leur semble trop fastidieux et ils décident alors de mesurer la valeur du champ magnétique B au centre de ce solénoïde. ils utilisent un teslamètre muni d'une sonde a effet Hall, mesurant la valeur de la composante du champ magnétique selon l'axe du solénoïde. Ils calculent alors N grâce à la relation B=4.(pi).10(puissance)-7.nI
La valeur mesurée est B= 0.560mT pour un courant d'intensité I= 1.80A.
1) La sonde utilisé doit elle être axiale ou tangentielle?
Justifié la réponse en indiquant la direction du champ magnétique au point considéré.
Quel serai le résultat de la mesure avec le type de sonde non adapté?
2) Est il important que le capteur de la sonde soit placé exactement au centre du solénoïde ? pourquoi?
3) Après calcul un élève trouve un nombre de spires égal a 248 et l'autre 149. Qui a raison?
Mes réflexions:
1) Je suppose que la sonde doit être axiale car le champs magnétique est uniforme...
2) ??
3) Je trouve 248 grâce à la formule: B=u0.n.L
Merci beaucoup !
Champ magnétique: solénoïde
2 messages
- Page 1 sur 1
Bonjour,
Tout d'abord, il faut que tu saches que la formule que l'on te donne est en fait une approximation. Cette formule est valable dans le cas d'un solénoïde de longueur infinie. Ce qui n'est bien évidemment pas le cas ici. On peut approximer la valeur du champ B au centre du solénoïde par cette formule si le rapport de la longueur du solénoïde sur son diamètre est suffisamment important (de l'ordre de 20 à 50). Ici, on ne te donne pas le rayon, mais vue la formule, on peut considérer que l'approximation est légitime.
Deuxième chose. Dans un solénoïde (de longueur finie ou non), le champ au centre dirigé selon l'axe du solénoïde. Pour un solénoïde de longueur infinie, le champ est uniforme partout dans le solénoïde et vaut effectivement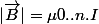 . Dans le cas d'un solénoïde fini, dont le rapport longueur sur diamètre est suffisamment élevé (le cas ici), on peut considérer quand dans le proche voisinage du centre, on a un champ uniforme, qui vaut aussi cette valeur. Mais attention !! Si le diamètre et la longueur sont du même ordre de grandeur, le champ ne peut plus être considéré comme uniforme dans le solénoïde, et cette formule ne s'applique plus.
. Dans le cas d'un solénoïde fini, dont le rapport longueur sur diamètre est suffisamment élevé (le cas ici), on peut considérer quand dans le proche voisinage du centre, on a un champ uniforme, qui vaut aussi cette valeur. Mais attention !! Si le diamètre et la longueur sont du même ordre de grandeur, le champ ne peut plus être considéré comme uniforme dans le solénoïde, et cette formule ne s'applique plus.
Enfin, dans la formule, n est le nombre de spires par unité de longueur. Ainsi, ta dernière réponse est fausse.
Tout d'abord, il faut que tu saches que la formule que l'on te donne est en fait une approximation. Cette formule est valable dans le cas d'un solénoïde de longueur infinie. Ce qui n'est bien évidemment pas le cas ici. On peut approximer la valeur du champ B au centre du solénoïde par cette formule si le rapport de la longueur du solénoïde sur son diamètre est suffisamment important (de l'ordre de 20 à 50). Ici, on ne te donne pas le rayon, mais vue la formule, on peut considérer que l'approximation est légitime.
Deuxième chose. Dans un solénoïde (de longueur finie ou non), le champ au centre dirigé selon l'axe du solénoïde. Pour un solénoïde de longueur infinie, le champ est uniforme partout dans le solénoïde et vaut effectivement
Enfin, dans la formule, n est le nombre de spires par unité de longueur. Ainsi, ta dernière réponse est fausse.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
