par ohanquez » 22 Déc 2010, 10:44
par Mathusalem » 22 Déc 2010, 13:30
ohanquez a écrit:Bonjour,
je souhaite réaliser moi même un support articulé pour ma TV mais je ne sais pas comment calculer les forces que cela va engendrer sur les fixations dans le mur.
Ma TV fait 20 kg et une fois le bras articulé ouvert au max, elle va se situer à 80cm du mur comme indiqué sur le plan en pièce joints.
Le bras fait lui une hauteur de 40cm
Le tout va être réalisé en tôle de 3mm donc le poids du bras articulé est négligeable
Merci pour vos lumières
Olivier
Bonnes fêtes de fin d'année
par ohanquez » 23 Déc 2010, 00:53
par Black Jack » 23 Déc 2010, 09:30
par Mathusalem » 23 Déc 2010, 09:58
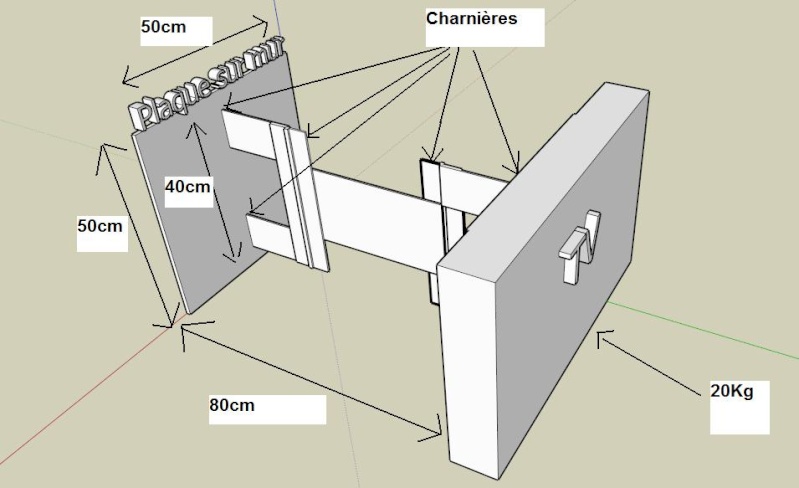
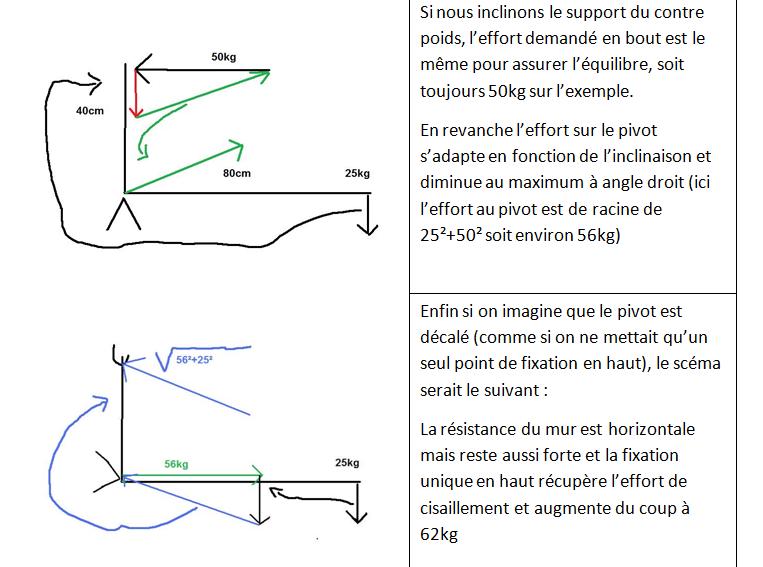
Black Jack a écrit:Ce moment devra être compensé par celui imposé par la force F du mur pour empêcher l'arrachage du point supérieur. Cette force agit avec un bras de levier de 40 cm (pour autant que la fixation soit la plus haute possible sur le support)
On a donc F*0,4 = 80
F = 200 N, soit 20 kgf
En pratique, on aura F très sensiblement plus grand que 20 kgf
:zen:
par Black Jack » 23 Déc 2010, 13:58
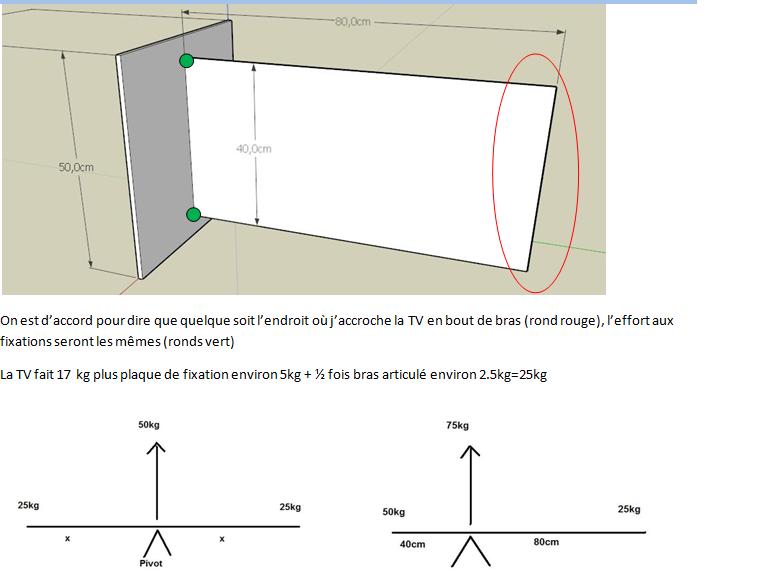
Mathusalem a écrit:C'est faux. Tu supposes que la force sur le point d'attache supérieur est entièrement vertical dirigé vers le bas, comme la gravité sur la télé. (en gros ta télé est entrain de tomber)
De plus, le centre de gravité, si tu négliges le mur, sera quasiment dans la télé.
Si tu comptes le mur, ce sera quasiment sur le mur (très massif).
Si tu prétends que ton centre de gravité est à 40 [cm] du support, par la définition du centre de gravité, un champ de force (g) a une résultante qui peut être considérée comme s'y appliquant. Donc, tu auras 20*g qui s'applique au centre de masse, et ton calcul part complètement en sucette, car t'as 0 moment dû à la télé, puisque tu t'es placé précisément à l'endroit où la gravité s'applique.
Le truc fourbe à faire pour un tel problème est de se placer à un point O qui serait un référentiel d'inertie. Par exemple, le point de pivot du système. Comme tu l'as dit, la réaction du mur sur le joint inférieur est pas très intéressant, c'est surtout l'arrachage sur le joint supérieur.
Si on se place au joint inférieur, que l'on considère comme le point de pivot, on obtient un moment de force dû à la gravité (qui pour ce problème s'applique sur le centre de la télé car le mur on s'en fout, c'est pas notre objet) de
M1 = 20*9.81*0.8 = 156.96 Nm
N'oublions pas le thm du centre de masse : puisque la télé est statique, si l'on considère 2 joints, il y a au moins une force de 10*9.81 verticalement vers le haut sur chacun des joints pour contrer la gravité. Il ne faudra donc pas oublier de rajouter 98.1 [N] (vectoriels) sur la force appliquée au joint.
Maintenant le point délicat, c'est de connaître l'orientation de la force du mur sur le joint pour l'empêcher d'arracher. En effet, on connaît le bras de levier, 0.4[m]. La réaction pure de 98.1[N] est colinéaire donc ne contribue pas.
Dans un modèle idéal, pour préserver le thm du centre de masse sur l'axe vertical, la composante de la force retient du mur est prise comme orthogonale au mur, comme ça l'addition vectorielle des forces maintient 98.1 [N] verticalement.
On a donc 0.4*F = 195.96 N[m]
F = 392.2 [N]
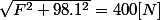
Plus ou moins 41 [kg].
Néanmoins le modèle est très idéalisé. En général la force de réaction sera pas orientée de cette manière et la force de réaction purement verticale sera plus grande que 10 [N]. Un facteur 2 n'est largement pas à écarter. Pour un calcul très précis, il faudrait beaucoup plus de détails quant aux grandeurs du problème.
En résumé, si tu pars sur une base de 80 [kg] t'es large.
par Mathusalem » 23 Déc 2010, 16:05
par Black Jack » 23 Déc 2010, 17:08
Mathusalem a écrit:Ce que je vois sur le schéma de Ohanquez (mannant ptet on dit la même chose et j'ai mal compris le schéma) :
Le point d'attache est séparé horizontalement de 80[cm] de la télé. Le poids s'applique sur la télé.
mgd = 20*g*[Distance qui separe le point d'attache de la télé], si on se fixe au point d'attache, ce que tu sembles avoir fait.
Dans ces conditions, le moment de force que la réaction que tu (Black Jack) dessines dans le mur, autour du pivot, vaut 0.4*F = 0.8*200 => F = 400 [N].
De plus, je ne pense pas que la force s'appliquant sur la fixation d'en haut soit complètement horizontale, mais que y a la composante verticale aussi, rien que pour supporter le poids de la télé. C'est pour ça que j'estime a 41-42 [kg] la charge sur le pivot, dans un modèle idéal.
Je répète, le centre de gravité est dans la télé si on suppose la tôle sans masse.
Quand à "verticale" j'ai pensé que tu t'es mis dans le centre de masse pour résoudre le problème, ce qui aurait constitué un truc très faux. Je pensais que tu disais que le centre de masse était à 40[cm]. De ce que j'ai compris de son schéma, a Ohanquez, tu t'es mis à égale distance entre la télé et le mur.
Néanmoins, je prends note que tu n'as pas pris la peine de lire ce que j'ai écrit, puisque nos résultats divergent d'un facteur 2 que tu ne commentes pas.
Je crois que t'as meilleur temps d'écouter ton quincailler
par ohanquez » 23 Déc 2010, 20:19
par Mathusalem » 23 Déc 2010, 21:15
par Black Jack » 24 Déc 2010, 11:33
Mathusalem a écrit:Avec une bonne approximation, ton centre de gravité se trouve à 75.6 [cm] du mur, et y agit un poids de 27 [kg] (Charnieres + plaque + tv).
On peut décrêter sans autres que le point de pivot sera le coin inférieur lié au mur. S'y placer pour faire une analyse du problème paraît pertinent. On évalue la tension d'arrachement maximale qui agit sur un piston, en restreignant le problème à un seul point d'attache 40 [cm] en-dessus du point de pivot.
En première approximation, la somme des moments nous mène à
0.756*27*9.81 = 0.4*Farrach
=> Farrach/g = 49 [kg] équivalents. si on considère la force d'arrachement normale au mur.
Ceci suppose que le point d'attache ne porte pas du tout le poids de la télé, et que ce travail est entièrement fait par le point pivot.
Je rajouterai par mesure de sécurité 10[kg] de charge sur le point d'attache, orienté tangentiellement au mur vers le haut. Ceci nous amène à 50 [kg] équivalents de charge sur le point pivot.
La tension d'enfoncement est selon moi bien supérieure, mais celle-ci n'est pas importante. Le matériau (acier) est très résistant à la compression et le mur encaisse parfaitement la poussée.
Cependant, mon instinct me dit la chose suivante :
Le point d'attache doit être fixé par un quelconque moyen dans le mur, par une vis par exemple. Selon moi, plus la vis est grosse et profonde, plus ce sera elle qui supporte la force d'arrachement et allègera la tension sur le point d'attache. Mais c'est que de l'instinct.
Moi je dirais que 50 [kg] +/- 15 [kg] sont raisonnables comme tension sur le point d'attache.
Cependant, je tiens à préciser que ton quinquailler n'est absolument pas en mesure de te donner une réponse à priori. S'il ne connaît pas les dimensions de l'objet fixé au mur, aucune chance qu'il te prédise la tension dans les joints. Donc c'est normal qu'il y ait un facteur d'environ 3 entre nos resultats et les siens... Par exemple, si ton bras coulissant faisait, au lieu de 40 [cm] , 4[m] de haut, tu imagines très bien toi même que la tension d'arrachement en haut est pratiquement nulle. Si en revanche elle ne faisait qu'un [cm], il faudrait te lever tôt pour trouver un mur qui sache faire ça
A+
Math
(je crois que Black Jack sera d'accord avec cette analyse)
par Mathusalem » 24 Déc 2010, 11:36
Black Jack a écrit:Le dessin complété lève les ambiguités.
Dans ces conditions :
Je trouve aussi G de l'ensemble à environ 75,7 cm du mur (avec une TV d'environ 10 cm d'épaisseur)
Ce qui amène à l'attache du haut dans le mur : Farrach/g = 51 kg (petite distarction dans la manip de la calculette, qui devrait donner aussi 51 kg)
F arrach étant la composante normale au mur de la force au niveau de l'attache supérieure.
Il y a aussi une composante verticale à cette force ... Mais on ne peut que l'estimer très grossièrement puisque les 2 attaches (haut et bas) reprennent les 27 kg en vertical mais on ne peut pas dire a priori dans quelle proportion.
La seule chose qu'on peut dire c'est que la somme des 2 composantes verticales aux points d'attache est de 27 kgf, la répartition entre les 2 points peut être n'importe quoi.
********
Attention que dans cette réflexion, les efforts dynamiques lors des manipulations ne sont pas pris en compte et que, de plus, on a vite fait lors de ces manip d'appliquer une composante verticale vers le bas sur la TV ...
Je ne suis pas un pro dans le calculs de fixation, mais il me semble qu'il faut au moins prévoir un coefficient de sécurité de 2 sur les forces calculées.
:zen:
par ohanquez » 24 Déc 2010, 14:53
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :
