Amplificateur opérationnel

[lecarpla]

Bonjour à tous!

Je suis en train de préparer un Contrôle Pratique d'électronique et j'aurais besoin qu'on vérifie mes résultat voir que l'on m'aide...

Voici l’énoncé



Et ce que j'ai fait pour l'instant



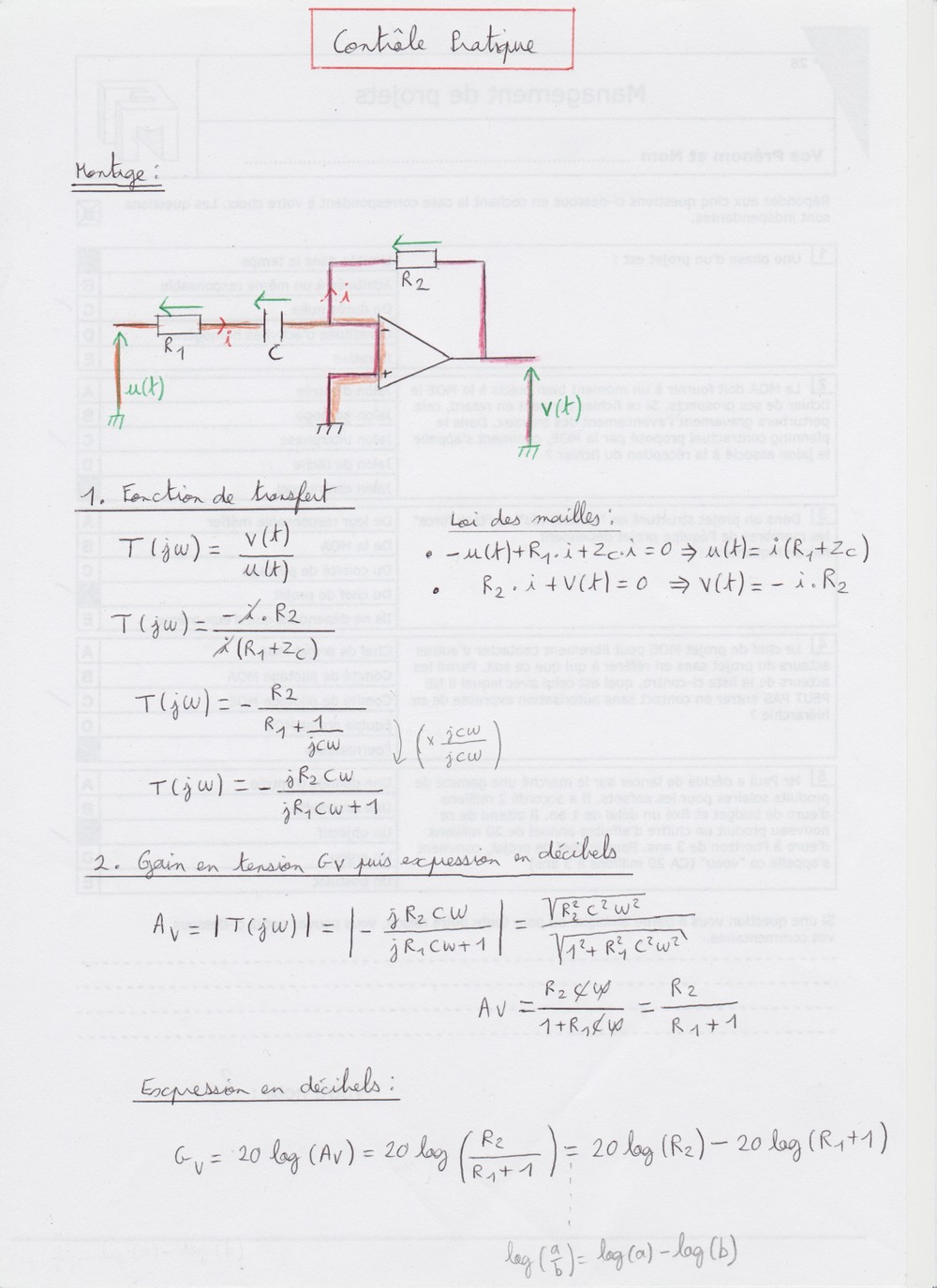
Je ferais le reste et le posterais prochainement mais je voulais déjà savoir si j'ai bon pour l'instant pour me rassurer Notamment pour la question 2 vu que la 1 je sais déjà que j'ai bon

Merci d'avance pour votre aide!

[Black Jack]

Av = wR2.C/racine(1 + w²R1²C²)

Gv = 20.log(wR2C) - 10.log(1 + w²R1²C²)

:zen:

[lecarpla]

Av = wR2.C/racine(1 + w²R1²C²)

Gv = 20.log(wR2C) - 10.log(1 + w²R1²C²)

:zen:

Merci de ton aide! Pourquoi laisse-t-on racine(1 + w²R1²C²) au dénominateur dans Av? Pour conserver w et C ensuite dans Gv?

Et la question suivante, je bloque :hein: On peux pas utiliser les log donc on reprends l'expression Av = wR2.C/racine(1 + w²R1²C²) et si on fais tendre w vers on tombe sur une forme indéterminée (;)/;)) où en travaillant un peu le calcul *0 ce qui n'est guère mieux...

[Black Jack]

lim(w --> +oo) Av = lim(w --> +oo) [wR2.C/racine(1 + w²R1²C²)] = R2/R1

lim(w --> +oo) Gv = 20.log(R2/R1)

:zen:

[lecarpla]

lim(w --> +oo) Av = lim(w --> +oo) [wR2.C/racine(1 + w²R1²C²)] = R2/R1

lim(w --> +oo) Gv = 20.log(R2/R1)

:zen:

A ce que j'ai pu lire ci et là, ton résultat à l'air bon mais je comprends pas pourquoi

lim(w --> +oo) Av = lim(w --> +oo) [wR2.C/racine(1 + w²R1²C²)] = R2/R1

J'ai certaines lacunes en limites il faut dire...

Parce qu'on à bien /;) si l'on fait tendre w vers l'infini non?

[lecarpla]

Haaa, j'ai peut être compris en fait! Je vérifie et si c'est ça, je poste ce que j'ai fait :)

[lecarpla]

Voilà ce que j'ai fait:



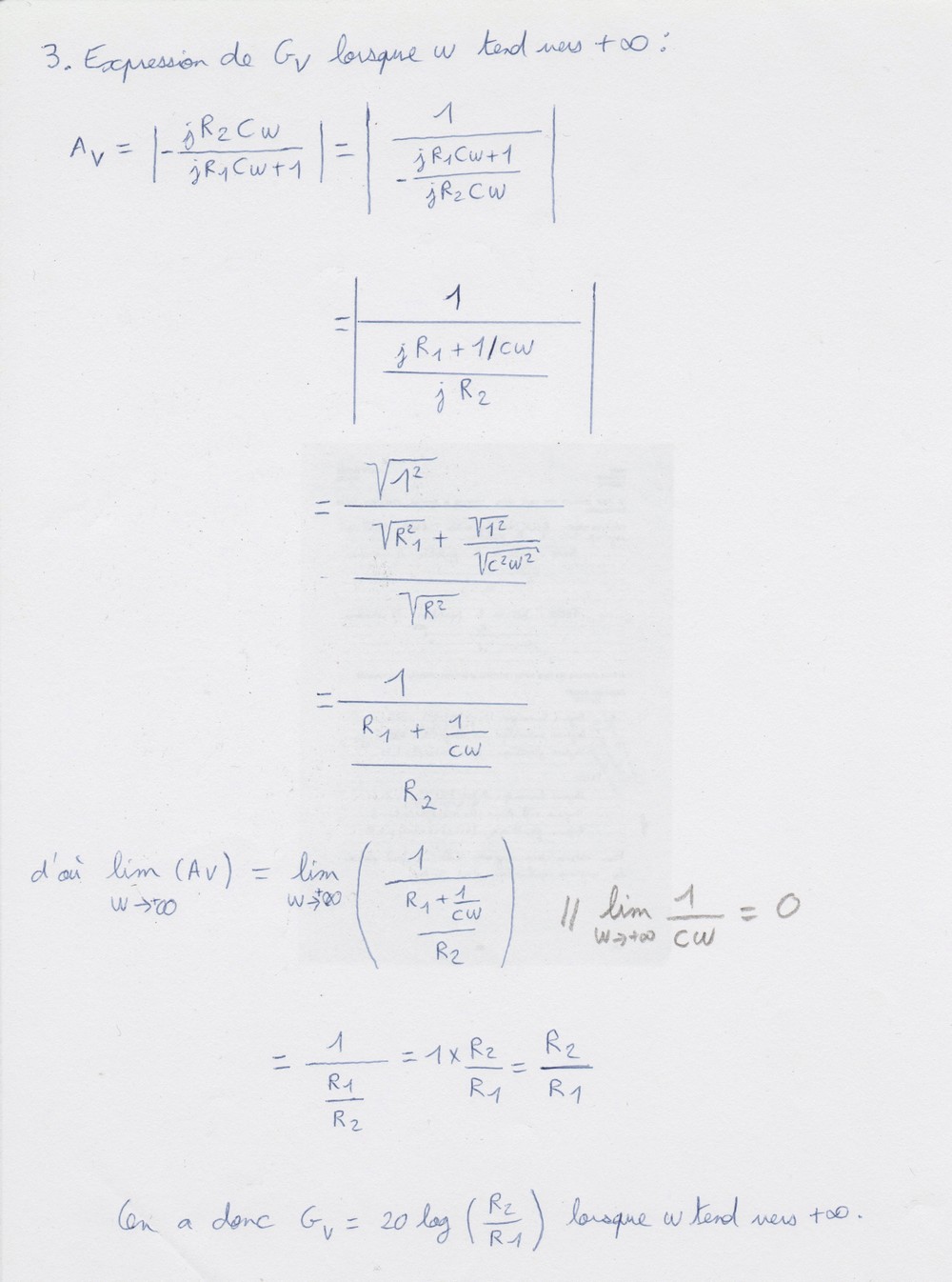
Et j'obtiens bien R2/R1 ce qui est rassurant...

Peut être une petite erreur de signe ou autres quelque part mais normalement non...

Allez hop, je passe à la 4!

[lecarpla]

Me voilà à nouveau bloqué...

Pour la 4, il faut bien dire qu'à la fréquence de coupure on a:

Av = Av(max) * 1/racine(2)?

Et en Av max on a bien R2/R1?

[lecarpla]

Je crois que j'ai compris!

J'ai pas le bon Av(max)!

C'est R2Cw le Av(max), c'est pour ça!!

Je trouve alors wc = 1/R1C c'est bien ça?

[lecarpla]

Et pour la 5 j'ai fait ça:



c'est tout bon pour la 4 et 5?

[Black Jack]

4) Attention, tu arrives à la bonne réponse ... mais en faisant de multiples erreurs en cours de route.

Le gain est max en hautre fréquence, |Av| max = R2/R1

Pulsation de coupure : pour |Av| = |Av|max/V2

wR2.C/racine(1 + w²R1²C²) = (1/V2).R2/R1
wR1.C/racine(1 + w²R1²C²) = (1/V2)
w²R1².C²/(1 + w²R1²C²) = (1/2)
2w²R1².C² = 1 + w²R1²C²
w²R1²C² = 1
wR1C = 1
wc = 1/(R1.C)

fréquence de coupure : fc = wc/(2.Pi)
fc = 1/(2.Pi.R1.C)
*****
5) Erreurs dans tes calculs.

R2/R1 = 2
1/(2.Pi.R1.C) = 1600

On doit fixer une valeur, par exemple la valeur de R1 et calculer le R2 et le C correspondants

R2 = 2.R1
C = 1/(3200*Pi.R1)

Exemple si on fixe par exemple R1 = 10^4 ohms, on calcule R2 = 2.10^4 ohms et C = 10 nF (arrondi)

[lecarpla]

Merci pour tout!

J’essaie de reprendre tout à 0. J'ai compris l'erreur pour la pulsation de coupure...

Je posterais mon travail quand j'aurais fini (ce soir ou demain).

Encore merci!

[lecarpla]

Ok, alors voilà les questions 1 à 4 refaites.





Normalement, c'est sans faute cette fois! :zen:

Pour la 5, je ferais ça un peu plus tard mais je posterais ce que j'aurai fait...

Pour la 6, 7, 8 c'est des manips donc on verra le jour J... :we:

Pour la 9, je dirais qu'il s'agit d'un montage dérivateur (le signal de sortie est la dérivée du signal d'entrée)

Encore merci Black Jack!! Ça m'aide vraiment!!

[Black Jack]

Attention, tu ne maîtrises pas les calculs d'élévation au carré ni le calcul pour le wc

Pour le calcul de wc, il faut partir du module du gain et pas de son expression complexe.

Ecrire -R2/(R1 + 1/(jCwc)) = (R2/R1) * (1/V2) est faux.
Le membre de droite est réel ... et le membre de gauche est complexe (et sa partie imaginaire non nulle).

Il FAUT partir de |R2/(R1 + 1/(jCwc))| = (R2/R1) * (1/V2)
|jCR2.wc/(jCR1.wc + 1)| = (R2/R1) * (1/V2)

qui donne : CR2.wc/racine(1 + wc²R1²C²) = (1/V2).R2/R1
Et on retombe sur le début de ma réponse précédente ...
********

Pour la 9 ...

Je dirais plutôt que c'est un filtre passe-haut.

Ce serait un dérivateur si on avait R1 = 0

:zen:

[lecarpla]

Pour le calcul de wc, je trouve comme les autres, 1/R1.C, t'es sûr que c'est pas bon?

Pour la remarque complexe à droite, réel à gauche tu as entièrement raison mais en fait, j'ai juste oublié de mettre le signe module autour de l'expression à gauche mais en dessous, c'est bien le module que j'ai pris. Et c'est le module de la fonction de transfert vu que -R2/(R1+1/jcw) c'est ce qu'on à au calcul de la fonction de transfert (question 1) juste avant de "simplifier" en multipliant le numérateur et le dénominateur par jcw.

Quant à la 9, il s'agit effectivement d'un filtre passe-haut mais il me semble que l'on peut dire que c'est un montage dérivateur au vu de ce que je peux lire sur ce site:
http://electronique.aop.free.fr/AOP_lineaire_F/Filtre_PHaut_1.html

Et des souvenirs d'un TP dont on a pas eu la correction malheureusement...

[lecarpla]

Ça y est, j'ai refait la 5 mais je tombe sur les même résultats que la première fois:



Si je prends R1 = 10^4 (et non pas 1000 comme je le fais), j'ai toujours R2 = 2R1 ce qui me donne R2=2.10^4 et pour C j'ai alors C = 1/(1600*10^4*2pi) ce qui me donne bien 10nF donc mes calculs sont bien les bons non?

[Black Jack]

Pour le calcul de wc, je trouve comme les autres, 1/R1.C, t'es sûr que c'est pas bon?
Pour la remarque complexe à droite, réel à gauche tu as entièrement raison mais en fait, j'ai juste oublié de mettre le signe module autour de l'expression à gauche mais en dessous, c'est bien le module que j'ai pris. Et c'est le module de la fonction de transfert vu que -R2/(R1+1/jcw) c'est ce qu'on à au calcul de la fonction de transfert (question 1) juste avant de "simplifier" en multipliant le numérateur et le dénominateur par jcw.

Quant à la 9, il s'agit effectivement d'un filtre passe-haut mais il me semble que l'on peut dire que c'est un montage dérivateur au vu de ce que je peux lire sur ce site:http://electronique.aop.free.fr/AOP_lineaire_F/Filtre_PHaut_1.html

Et des souvenirs d'un TP dont on a pas eu la correction malheureusement...

Sûr que la réponse finale est la bonne, mais il y a plusieurs erreurs pour y arriver.

Il manque les "modules" dès le début.

Et de très sérieuses erreurs par la suite.

Passer de -R2/(R1+1/(jCwc)) = R2/R1 * 1/V2 à 1/(R1 + 1/(Cwc)) = 1/(R1.V2) est une monstruosité.

Passer de 1 + 1/CwcR1 = V2 à 1 + 1/C²wc²R1² = 2 est une monstruosité.

Etc ...

Bref, de multiples erreurs.
On se demande alors comment tu arrives à une expression finale juste.

Mais si tu écris cela (avec les erreurs), avec un prof qui prend le temps de lire ce que tu écris, tu te feras ratiboiser.


Et bien pas vraiment, c'est certes un schéma analogue ... mais il ne se comportera presque comme un dérivateur que si R1 est quasi nul, donc pour un R2/R1 très très élevé.
Or ici, on demande R2/R1 = 2 ... Et dès lors, le circuit se comporte en filtre passe-haut et pas du tout en dérivateur.

:zen:

[Black Jack]

Ça y est, j'ai refait la 5 mais je tombe sur les même résultats que la première fois:

Et bien non, encore erreurs de calcul. (dans la partie écrite en bleue)

Tu écris C = 1/(1600*1000*2Pi)

C = 10.10^-8 F ... et tu conclus erronément que C = 1 nF

Raté, C = 10.10^-8 F est égal à 100 nF et pas ce que tu as écrit.

:zen:

[lecarpla]

Oui effectivement, petit problème de traduction de puissance... Au passage, un site très bien pour la conversion en Farad, µF, nF etc... si quelqu'un en a besoin:

http://www.convertworld.com/fr/capacite-electrique/Farad.html

Quand à moi, j'ai refais mes calcul sans trop refaire les règles mathématiques cette fois-ci... mon contrôle pratique est demain, je tâcherais de scanner ma copie une fois qu'elle me sera rendu pour ce à qui ça pourra être utile...

Encore merci!!

[lecarpla]

Au final, on a eu un autre contrôle pratique que celui que j'ai préparé... Je sais pas trop ce que ça a donné... J'ai du bon, et du moins bon... mais ça m'aura bien aidé de m’entraîner sur celui-ci en tout cas! :) merci pour tout!