D'où vient la formule de la variance ?

[Gurvan44]

Bonjour à tous je ne trouve pas de démonstration de la formule la plus connue de la variance ou une explication de son origine.

V(x) = [somme((xi - moyenne)^2)]/n
Si qq a une piste

[capitaine nuggets]

Salut !

, où désigne l'espérance : , on peut parfois la noter .

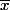
[zygomatique]

salut

il n'y a pas de démonstration !!! c'est une définition ...

la variance est un cas particulier des moments centrés : c'est le moment centré d'ordre 2 ...

l’espérance est le moment d'ordre 1 ....

[pascal16]

V(x) = [somme((xi - moyenne)^2)]/n
V(x) = [somme((xi² -2xi* moyenne+moyenne²))]/n
V(x) = [somme(xi²) -2somme(xi* moyenne)+somme(moyenne²)]/n
V(x) = [somme(xi²) -2n*moyenne*somme(xi)+n*moyenne²]/n
V(x) = [somme(xi²) -2n*moyenne*moyenne+n*moyenne²]/n
V(x) = [somme(xi²) -2n*moyenne²+n*moyenne²]/n
V(x) = [somme(xi²) -n*moyenne²]/n
V(x) = [somme(xi²)]/n -moyenne²
V(x) = E(X²)-(E(X))²

[zygomatique]

là on démontre quelque chose ... mais on démontre autre chose : la formule de Koenig ...

[Gurvan44]

Merci pour vos réponses, ce ne serait qu'une définition alors.. une convention mais je n'ai pas encore entendu parler de ces moments centrés d'ordres multiples, peut-être me faudra-t-il cette notion pour en comprendre le sens de cette variance...
Car pour le moment à la différence de l'espérance qui a un sens assez évident et une formule intuitive, je trouve que la Variance n'est pas vraiment analogue.

Je suis en train de revoir toutes les maths jusque la Terminale en détail et en profondeur, mais je pense que je laisserai les stats et proba pour la fin car elles me semblent les plus complexes à décortiquer !

[beagle]

wikiki:"On peut interpréter la variance comme la moyenne des carrés des écarts à la moyenne (rigoureusement : l'espérance des carrés des écarts à l'espérance, informellement : moyenne des carrés moins le carré de la moyenne).

Elle permet de caractériser la dispersion des valeurs par rapport à la moyenne. Ainsi, une distribution avec une même espérance et une variance plus grande apparaîtra comme plus étalée. Le fait que l'on prenne le carré de ces écarts à la moyenne évite que des écarts positifs et négatifs ne s'annulent."

.................................................................

si tu cherches comment se dispersent les valeurs par rapport à la moyenne,
ben tu regardes l'écart à la moyenne, et ensuite tu feras la moyenne de ces écarts.
Bon la mise au carré complique un peu la compréhension, mais on voit bien que l'on étudie les écarts par rapport à la moyenne dans cette formule.

[zygomatique]

ce n'est pas une interprétation !! c'est une définition !!!

la variance est la moyenne des carrés des écarts à la moyenne

PS : en proba on dit (évidemment) espérance au lieu de moyenne qui est un terme statistique, on fait donc un abus de langage ... fort naturel ...

d'autre part se rappeler que l'espérance et la variance sont elles-même des variables aléatoires ... (des estimateurs)

[beagle]

"ce n'est pas une interprétation !! c'est une définition !!!"

je ne comprends pas
cette définition raconte bien quelque chose, c'est ce qui est écrit la ligne suivante qui est interprétation
c'est juste que le gars sur ce sous-chapitre dit de quoi cela parle.La première phrase tu as raison est la définition...

[Gurvan44]

Ok je comprend donc comment on en est arrivé à cette formule c'était surtout le carré que je ne saisissais pas. Très bien et je peux en conclure que l'écart-type est donc plus interprétable car il équilibre la mise au carré en faisant la racine carré de la variance ?

Et si c'est une définition alors comment se fait-il qu'il existe plusieurs formules ? se valent-t-elles toutes ?
Je pense que pour comprendre la réponse à cette question je suis encore un peu trop novice en stats et proba et que je dois attendre de voir les choses petit à petit... (je viens de finir ma L1 Physique).

Dernière chose si vous avez des adresses (sites,vidéos ...) sympas qui expliquent des thèmes de maths en partant plus ou moins des fondamentaux je serai très intéressé !

[capitaine nuggets]

Et si c'est une définition alors comment se fait-il qu'il existe plusieurs formules ? se valent-t-elles toutes ?

En fait, ça dépend de ce qu'on te donne comme définition. Ca peut dépendre du contexte.
Si on t'a défini la variance comme la formule que tu donnes alors il n'y a rien à montrer puisque c'est une définition ; si on t'a défini la variance par une autre formule alors la formule que tu donnes peut-être justifiée.

[pascal16]

Là tu as la formule pour une liste de nombres fini (dite variable discrète).
Tu as aussi une variance pour des densité de probabilité (comme la loi normale ou exponentielle).

Les définitions son telles que si une loi loi discrète (du Binomiale au hasard) tend vers une loi continue (du loi normale au hasard), la variance de la loi discrète converge vers celle de la loi continue.

les formules du type variance(aX+b) marchent aussi dans les deux cas.

[Pseuda]

Bonsoir,

C'est une question qui revient souvent, je me l'étais posée :

superieur/ecart-type-t174427.html

Passe les passages que tu ne comprends pas. Par rapport à d'autres mesures de dispersion (par exemple la somme des valeurs absolues des écarts à la moyenne, au lieu de la somme des carrés des écarts), la variance et sa racine carrée l'écart-type a une affinité certaine avec la loi normale et réagit mieux à certains calculs (par exemple somme de variables indépendantes), en plus d'être plus pratique pour les calculs. Cela en fait une mesure de dispersion plus "naturelle".

[zygomatique]

le sujet diverge vers des choses sans lien avec la question ...

[Pseuda]

le sujet diverge vers des choses sans lien avec la question ...

Je pense pourtant que cette réponse est tout à fait en lien avec la question de Gurvan44 :

Merci pour vos réponses, ce ne serait qu'une définition alors..

Car pour le moment à la différence de l'espérance qui a un sens assez évident et une formule intuitive, je trouve que la Variance n'est pas vraiment analogue.

Cette question revient souvent dans la tête de ceux qui se posent des questions.

[zygomatique]

je ne parlais pas de toi et de ton lien en rapport effectivement ... mais plutôt du dernier msg de pascal16

pour finir la variance ne pose pas de pb :

l'espérance est une moyenne
la variance est une moyenne (voir définition en français plus haut)
un moment est une moyenne

après on centre ces moments ou pas ...

plus généralement la moyenne des puissances p-ième des modalités d'un caractère est ... une moyenne


dans le cas où p = 2 on retrouve la formule de Koenig qui donne le lien entre le moment centré d'ordre 2 (la variance) et la moyenne des carrés des valeurs ...

[pascal16]

pour ce qui est "moment d'ordre 1"

si on on place un poids de 2kg à l'abscisse -3 et un poids de 5kg à l'abscisse 2, la moyenne trouvée est l'emplacement où l'on doit placer l'axe pour que le système soit en équilibre. Le mot moment est bien le même qu'en physique.


Pour la variance et l'écart type. L'écart-type a la même unité que celle du caractère étudié, c'est donc l'écart-type qui sert pour interpréter les résultats. Si on a une loi normale, on sait déterminer graphiquement l'écart type.