Vérification exo réel a et équation de droite

[kenymi]

Bonjour,

Pouvez-vous verifier si tout est correct ? Merci.

Le plan est rapporté à un repère ((O; ;);)i ; ;);)j ). Pour tout réel a,*on considère la droite ;)a d'équation : (a + 2 )x + (a² - 1 )y + a² + a + 1 = 0*.

Déterminer si elles existent les valeurs de a pour lesquelles ;)a

a) Est parallèle à l'axe des ordonnées
b) Est parallèle à l'axe des abscisse
d) Admet pour vecteur directeur ;););)u = ;););)i + 2j;);)

a) D// à l'axe des ordonnées donc x=c et y=0
y=0 si et seulement si a² - 1=0 si et seulement si a=^1 ou a=-^1

b) D// à l'axe des abscisses donc y=c et x=0
y=c si et seulement si a + 2=0 si et seulement si a=-2

c) u=i+2j donc u(-b;a) u(-2;a)


(a + 2 )x + (a² - 1 )y + a² + a + 1 = 0*.

u'(-b;a) u'(-a^2+1;a+2)

(-a^2+1)a -(-2)(a+2)=0

---> Je coince ici car ça me parait bizarre d'avoir des a^3...


Merci pour votre aide!

[chan79]

salut

Pour a) et b), c'est bon
Un vecteur directeur de la droite a comme coordonnées (1-a²,a+2)
Il doit être colinéaire à (1,2)

2(1-a²)=a+2 ce qui donne deux valeurs

Une remarque
L'équation s'écrit a(x+1)+a²(y+1)+(2x-y+1)=0

on s'aperçoit que si (x;y)=(-1;-1) l'équation est toujours vérifiée (quelle que soit la valeur de a).

Autrement dit, les droites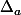 passent toutes par le point (-1;-1)

[maths-lycee fr]

Bonjour,

Pouvez-vous verifier si tout est correct ? Merci.

Le plan est rapporté à un repère ((O; ;)i ; ;)j ). Pour tout réel a,*on considère la droite a d'équation : (a + 2 )x + (a² - 1 )y + a² + a + 1 = 0*.

Déterminer si elles existent les valeurs de a pour lesquelles a

a) Est parallèle à l'axe des ordonnées
b) Est parallèle à l'axe des abscisse
d) Admet pour vecteur directeur ;);)u = ;);)i + 2j;);)

a) D// à l'axe des ordonnées donc x=c et y=0
y=0 si et seulement si a² - 1=0 si et seulement si a=^1 ou a=-^1

b) D// à l'axe des abscisses donc y=c et x=0
y=c si et seulement si a + 2=0 si et seulement si a=-2

c) u=i+2j donc u(-b;a) u(-2;a)


(a + 2 )x + (a² - 1 )y + a² + a + 1 = 0*.

u'(-b;a) u'(-a^2+1;a+2)

(-a^2+1)a -(-2)(a+2)=0

---> Je coince ici car ça me parait bizarre d'avoir des a^3...


Merci pour votre aide!

Bonjour,

Pour la fin, tu as mélangé deux choses:



signifie que et non (-b;a) comme tu l'as écrit.

Un vecteur de coordonnées (-b;a) est un vecteur directeur de la droite d'équation cartésienne ax+by+c=0....ce que tu as bien écrit ensuite pour le vecteur u'...

[kenymi]

Ah oui !! D'accord,merci beaucoup ! Donc,lorsqu'un vecteur directeur s'écrit sous la forme u(-b;a),il peut également s'écrire sous la forme u=-by+ax ?

[maths-lycee fr]

Ah oui !! D'accord,merci beaucoup ! Donc,lorsqu'un vecteur directeur s'écrit sous la forme u(-b;a),il peut également s'écrire sous la forme u=-by+ax ?

Bonjour,

je ne comprend pas très bien ta remarque mais je crois que c'est toujours un peu confus...

Le vecteur u=1i+2j n'a rien à voir avec les équations de droites.

Dire qu'un vecteur dans le repère signifie que (on a ici x=1 et y=2)