Vecteurs&Valeurs propres

[MaxQuébec]

Cours: algèbre linéaire et vectoriel

Bonjour,

j'en suis à une première apparition sur les pages de ce forum. J'accroche quelque peu avec les concepts de valeurs propres et vecteurs propres. Même après une lecture de bouquins, l'idée reste vague. Certes, je comprends ce que c'est, mais j'ai peine à utiliser correctement l'algorithme pour les trouver... (Un exemple me démerderait probablement)

Voilà quand même la question. Je me fiche de la réponse, mais j'aimerais connaitre le bon chemin.

Trouver vecteurs et valeurs propres de cette matrice

| 3 1 0 |
|16 -3 0 |
| 0 0 -7 | ( désolé pour cette piètre matrice )

Je commence par où? Je sais que le vecteur et la valeur propres sont un vecteur et une constante tel que la multiplication de la matrice par le vecteur égale la multiplication de la constante par ce même vecteur...


Merci d'avance.
Max

[Mathusalem]

Sauf erreur de ma part :

Ajoute un - sur chaque terme de la diagonale.

Calcul ensuite le discriminant de ta matrice, ce qui te donnera un polynome caracteristique de la forme etc..
Mets le = 0
Tu as donc une equation caracteristique maintenant. Cherche les qui satisfont ton equation.
En general, tu auras
pour une matrice 3x3

Ensuite, des que tu as tes valeurs distinctes, tu veux calculer les sous-espaces propres : Remplace par sa vraie valeur dans ta matrice. Si ta valeur propre est de multiplicite 1 (c'est-a-dire que ton polynome n'a qu'un seul terme en ( - la valeur precise)), alors cela engendrera un sous-espace de dimension 1.

Pour verifier que ta matrice est bien diagonalisable, il faut que la somme des dimensions des sous-espaces corresponde a la dimension de l'application. En d'autres termes, a chaque valeur propre de multiplicite n doit etre associe un sous-espace propre de dimension n.

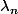
Si tu ne sais pas comment calculer un sous-espace propre, tu as trop d'avance dans le cours par rapport a ce que tu dois faire (c'est calculer l'image d'une application, en l'occurence ici, l'application (M - Id)

Tes sous-espaces sont composes de vecteurs, en l'occurence, de n vecteurs selon leur n dimension. Tous ces vecteurs sont des vecteurs propres.

Donc. Tu as le choix : Soit tu dis que ta matrice diagonale est
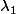
| 0 0 |
|0 0 |
|0 0 |
Ce que tu es en principe autorise a faire

Ou tu utilises que ou P est la matrice de passage, M ta matrice, et M' ta matrice diagonalisee
=> Tu obtiendras le meme resultat, a une condition pres.

Ta matrice de passage contient les vecteurs propres en colonne dans un certain ordre.
Si tu as en colonne dans ta matrice de passage le vecteur propre associe a ta premiere valeur propre, alors tu auras comme premier terme de la diagonale ta premiere valeur propre. En d'autres termes, il faut etre consistant.

Tu peux dire que ta matrice est comme je l'ai marquee plus haut, sans donner le detail du calcul, mais dire qu'elle est comme ca, pour autant qu'on assume une base (Vecteur propre associe a la premier valeur propre de la diagonale ; Vecteur propre associe a la deuxieme valeur propre de la diagonale ; Vecteur propre associe a la 3e valeur propre de la diagonale).
=> L'ordre compte

J'espere que c'est clair.

A+


PS: La theorie de pourquoi ca marche remonte jusqu'aux calculs de noyau (Ker) donc si tu veux t'instruire, faudra lire, et lire beaucoup