Vecteurs et reperage dans l'espace

[marion7]

bonjour,

Je suis face a un problème de coordonnées,
voici l'énoncé :

A(2;1;0) B(0;1;1) et C(0;3;2)
La droite passant par 0(0;0;0) et de vecteurs dircteur k(0;1;1) coupe donc le plan (abc). Soit I le point d'intersection. determinez ses coordonnées.

[lexot]

Bonjour

Où sont tes résultats?
Quelques pistes :
(-2;0;1) ; 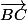(0;2;1)

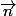(1;-1;2) est normal aux vecteurs AB et BC, donc normal au plan ABC (produit scalaire nul)

Soit M(x;y;z) élément du plan ABC =>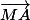 (x-2;y-1;z)
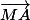normal à =>

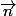équation du plan ABC : x-y+2z-1 = 0

La droite de vecteur directeur k vérifie le système :
x = 0
y = t
z = t

Le point I(0;1;1), vérifie le système (t=1), et l'équation du plan ABC. Il est confondu avec le point B

Cordialement

[flight]

salut


pour trouver l'équation du plan passant par les points A,B et C

on peut ecrire qu'il existe M(x,y,z) et (µ,j) appartenant à R² tels que

MA=µMB+jMC sous forme d'expression vectorielle.

soit x-2=-2µ-2j
y-1= 2j
z= µ+2j.


soit x-2= -2µ-y+1
et z= µ+y-1 ou 2z= 2µ+2y-2


x-2+2z=y-1 soit x-y+2z=1.