Vecteurs colinéaires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par Azertyuiop32 » 31 Oct 2013, 22:26
par Azertyuiop32 » 31 Oct 2013, 22:26
Bonjour, je bloque sur un exercice, je sais pas comment m'y prendre:
A B C D, quatre points tels que: 3AD=AB+2AC
1) faire la figure
2) Démontrez que B C D sont alignés.
Pour la figure je trouve une droite dont les points sont dans cet ordre : A C D B et distants en fonction des mesures de l'énoncé mais je ne sais pas si c'est bon.
Ensuite je ne voit pas comment prouver que les points sont alignés, donc colinéaires.
Merci de m'éclairer :)
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 31 Oct 2013, 22:50
par siger » 31 Oct 2013, 22:50
bonsoir
si trois points B, C et D sont alignes on doit avoir des vecteurs colineaires : par exemple
BC = k*BD
BC = BA + AC
BD = BA + AD
d'autre part 3AD = AB +2AC + AC -AC = AB -AC + 3AC = 3AC - BC
......
 par Azertyuiop32 » 31 Oct 2013, 23:02
par Azertyuiop32 » 31 Oct 2013, 23:02
Désoler mais je pense que ma figure est fausse car je ne comprend pas ce que tu as fait. Il faut développer 3AD=AB+2AC pour arriver à BC=k*CD ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 01 Nov 2013, 06:46
par Shew » 01 Nov 2013, 06:46
Azertyuiop32 a écrit:Bonjour, je bloque sur un exercice, je sais pas comment m'y prendre:
A B C D, quatre points tels que: 3AD=AB+2AC
1) faire la figure
2) Démontrez que B C D sont alignés.
Pour la figure je trouve une droite dont les points sont dans cet ordre : A C D B et distants en fonction des mesures de l'énoncé mais je ne sais pas si c'est bon.
Ensuite je ne voit pas comment prouver que les points sont alignés, donc colinéaires.
Merci de m'éclairer

Bonjour
On a

et

Dans la formule de l'énoncé il en résulte
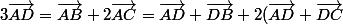 = \vec{AD} + \vec{DB} + 2\vec{AD} + 2\vec{DC} \\ = 3\vec{AD} + \vec{DB} + 2\vec{DC} \Leftrightarrow 3\vec{AD} - 3\vec{AD} = \vec{DB} + 2\vec{DC} \Leftrightarrow \vec{DB} + 2\vec{DC} = 0 \\ \Leftrightarrow \vec{DB} = -2\vec{DC} \Leftrightarrow \vec{DB} = 2\vec{CD})
.
Il ne reste plus qu'à conclure .
 par Azertyuiop32 » 01 Nov 2013, 07:35
par Azertyuiop32 » 01 Nov 2013, 07:35
Shew a écrit:Bonjour
On a

et

Dans la formule de l'énoncé il en résulte
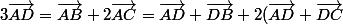 = \vec{AD} + \vec{DB} + 2\vec{AD} + 2\vec{DC} \\ = 3\vec{AD} + \vec{DB} + 2\vec{DC} \Leftrightarrow 3\vec{AD} - 3\vec{AD} = \vec{DB} + 2\vec{DC} \Leftrightarrow \vec{DB} + 2\vec{DC} = 0 \\ \Leftrightarrow \vec{DB} = -2\vec{DC} \Leftrightarrow \vec{DB} = 2\vec{CD})
.
Il ne reste plus qu'à conclure .
Merci beaucoup! Je peut donc conclure qu'ils sont colinéaires
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 01 Nov 2013, 07:37
par Shew » 01 Nov 2013, 07:37
Azertyuiop32 a écrit:Merci beaucoup! Je peut donc conclure qu'ils sont colinéaires
Oui et s'ils sont colinéaires alors ....

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 01 Nov 2013, 07:49
par chan79 » 01 Nov 2013, 07:49
Salut
On peut voir que D est le centre de gravité d'un triangle dont (BC) est une médiane
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Nov 2013, 15:53
par siger » 01 Nov 2013, 15:53
Azertyuiop32 a écrit:Désoler mais je pense que ma figure est fausse car je ne comprend pas ce que tu as fait. Il faut développer 3AD=AB+2AC pour arriver à BC=k*CD ?
Re
Je pensais qu'il fallait te laisser un peu de travail....!
sinon
3AD = 3AC + AB -AC
3(AD - AC) = (AB - AC)
ou 3 CD = CB
...........
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 129 invités
