Vecteur de l'espace

[NatNat]

Bonjour, je suis en terminale et je bloque sur l'exercice suivant :
ABCD est un tétraèdre.
I, J, K, L, M et N sont les milieux respectifs des
arêtes [AB], [CD], [BC], [DA], [BD] et [AC].
1) Démontrer que les segments [IJ], [KL] et
[MN] ont le même milieu E.
2) En déduire que EA+EB+EC+ED=0
3) Quelles sont les coordonnées de E dans le
repère (A;AB;AC;AD) ?
(a) Donner les coordonnées des vecteurs EI, EK et EM dans le
repère (A;AB;AC;AD) ?
(b) Vérifier que ( E,EI,EK,EM) est un repère de l'espace.
5) Quelles sont, dans le repère ( E,EI,EK,EM), les coordonnées des sommets A, B, C et D du
tétraèdre ?
Merci d'avance
Cordialement

[Ben314]

Salut,
A mon sens, c'est un exercice de base sur les vecteurs de l'espace de dimension 3.
Pour la question 1), la méthode sans doute la plus naturelle (mais pas forcément la plus simple), c'est de définir le point E comme étant le milieu de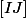 donc, par construction, on a puis de démontrer que c'est aussi le milieu de , c'est à dire que .
Et bien évidement, il faut utiliser la relation vu que c'est la seule chose qu'on connait concernant (et tout aussi évidement, il faut utiliser les définitions de ainsi que la relation de Chasles)

[NatNat]

Salut,
A mon sens, c'est un exercice de base sur les vecteurs de l'espace de dimension 3.
Pour la question 1), la méthode sans doute la plus naturelle (mais pas forcément la plus simple), c'est de définir le point E comme étant le milieu de donc, par construction, on a puis de démontrer que c'est aussi le milieu de , c'est à dire que .
Et bien évidement, il faut utiliser la relation vu que c'est la seule chose qu'on connait concernant (et tout aussi évidement, il faut utiliser les définitions de ainsi que la relation de Chasles)

Merci de votre réponse, mais y a t'il une méthode plus simple car j'avoue que je ne vois pas comment prouver ceci une fois le nez sur ma copie...