Bonjour à vous,
Je suis bloqué à mon dm de maths à la question 2b
J'ai longuement réfléchi, et j'ai trouvé comme solution le théorème de Thalès ou le théorème de Pythagore. Mais parmi les deux, on n'a pas assez de données pour pouvoir utiliser la formule (déjà, si c'est bien ça...)
Merci de m'éclairer ! ^^
LE DM : https://ibb.co/x86Vqcx
Variations et extrema d'une fonction [DM]
7 messages
- Page 1 sur 1
Re: Variations et extrema d'une fonction [DM]
Bonjour
Le théorème de Pythagore et vous aurez remarqué que
les angles intérieurs d'un triangle équilatéral valent 60° et que le cosinus de 60° est
à partir de là il devient facile de poser une équation qui donne AQ à partir de x et ensuite de poser Pythagore
Le théorème de Pythagore et vous aurez remarqué que
les angles intérieurs d'un triangle équilatéral valent 60° et que le cosinus de 60° est
à partir de là il devient facile de poser une équation qui donne AQ à partir de x et ensuite de poser Pythagore
Re: Variations et extrema d'une fonction [DM]
[quote="azf"]
Merci pour votre réponse !
En effet, je n'avais pas eu cette clairvoyance concernant les angles..
Désormais, je suis bloqué pour l'"équation" que vous avez évoqué. J'ai cherché mais aucun résultat logique..
Pouvez-vous m'éclaircir ? Merci
Merci pour votre réponse !
En effet, je n'avais pas eu cette clairvoyance concernant les angles..
Désormais, je suis bloqué pour l'"équation" que vous avez évoqué. J'ai cherché mais aucun résultat logique..
Pouvez-vous m'éclaircir ? Merci
Re: Variations et extrema d'une fonction [DM]
Bonjour
je ne peux pas vous la donner cette équation il faut que vous la cherchiez
je peux essayez de vous l'indiquer un peu plus (je pensais avoir tout dit mais bon on peut essayer):
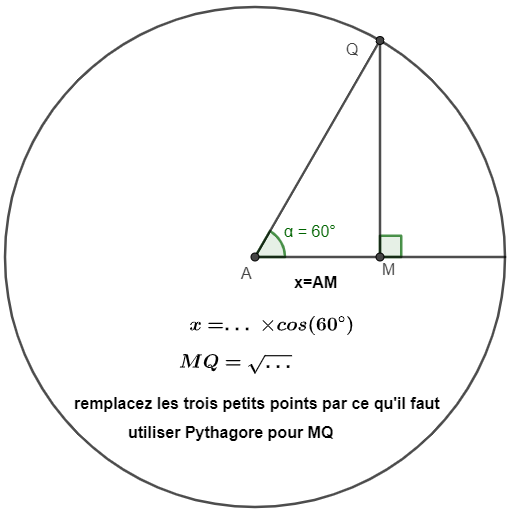
je ne peux pas vous la donner cette équation il faut que vous la cherchiez
je peux essayez de vous l'indiquer un peu plus (je pensais avoir tout dit mais bon on peut essayer):

Re: Variations et extrema d'une fonction [DM]
Bonjour,
quand on connaît la longueur du côté du triangle équilatéral on en déduit la hauteur du triangle et en utilisant Thalès on obtient le réponse en 1 seule équation
quand on connaît la longueur du côté du triangle équilatéral on en déduit la hauteur du triangle et en utilisant Thalès on obtient le réponse en 1 seule équation
Re: Variations et extrema d'une fonction [DM]
Bonjour
Pourquoi passer par le cosinus ? La tangente me semble plus appropriée.
Pourquoi passer par le cosinus ? La tangente me semble plus appropriée.
Re: Variations et extrema d'une fonction [DM]
catamat a écrit:Bonjour
Pourquoi passer par le cosinus ? La tangente me semble plus appropriée.
c'cst vrai aussi et c'est même mieux
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
