Explication sur les extrema

par **choup** » 03 Oct 2009, 17:04

Bonjour,

Je n'ai pas très bien compris le cours sur les extremums pouvez-vous me l'expliquer sur un exemple simple du type f(x) = X^3 - X
Merci d'avance

PS : attention : un extremum, des extrema. je sais bien qu'on ne fait plus beaucoup de latin, mais quand même !

par **Billball** » 03 Oct 2009, 17:06

bah qu'est ce que tu comprends pas? c'est assez vague la?

par **Laurent Porre** » 03 Oct 2009, 17:45

salut
aux extrémums (locaux), la dérivée s'annulle et change de signe.
Je suppose que tu sais comment dériver la fonction que tu as donnée. Donc tu devrais facilement pouvoir trouver les extrémums

par **choup** » 03 Oct 2009, 19:18

oui je sais la dériver : f'(x) = 3X(^2)-1 en fait c'est juste que je savais pas comment procéder pour trouver un extremum quel été la démarche à suivre.
merci pour votre aide !

par **Dominique Lefebvre** » 03 Oct 2009, 19:20

choup a écrit:oui je sais la dériver : f'(x) = 3X-1 en fait c'est juste que je savais pas comment procéder pour trouver un extremum quel été la démarche à suivre.
merci pour votre aide !

Bonsoir,
ta dérivée est fausse....

par **Dominique Lefebvre** » 03 Oct 2009, 19:22

choup a écrit:oui je sais la dériver : f'(x) = 3X-1 en fait c'est juste que je savais pas comment procéder pour trouver un extremum quel été la démarche à suivre.
merci pour votre aide !

Une fonction f présente un extremum (minimum ou maximum) pour chaque point sur lequel sa dérivée f' s'annule. C'est un théorème à savoir. On détermine s'il s'agit d'un max ou d'un min en étudiant sa dérivée seconde f".

par **choup** » 03 Oct 2009, 19:26

Merci beaucoup ! et pour la dérivée en effet j'ai écris vite j'ai pas fais attention je viens de la corriger !

par **Dominique Lefebvre** » 03 Oct 2009, 19:31

choup a écrit:Merci beaucoup ! et pour la dérivée en effet j'ai écris vite j'ai pas fais attention je viens de la corriger !

OK et donc ta fonction admet combien d'extrema? qui sont?

par **choup** » 03 Oct 2009, 19:32

En fait j'étudie le signe de f''(x) c'est sa ? donc si c'est positif c'est un maximum et si c'est négatif c'est un minimum ou pas ?

par **choup** » 03 Oct 2009, 19:36

Elle s'annule pour x= racine de 1/3 donc racine de 1/3 est un extremum

par **Dominique Lefebvre** » 03 Oct 2009, 19:36

choup a écrit:En fait j'étudie le signe de f''(x) c'est sa ? donc si c'est positif c'est un maximum et si c'est négatif c'est un minimum ou pas ?

Oui, mais il faut déjà identifier les extrema, en trouvant pour quels x la dérivée s'annule....

par **Dominique Lefebvre** » 03 Oct 2009, 19:42

choup a écrit:Elle s'annule pour x= racine de 1/3 donc racine de 1/3 est un extremum

Tu es sur qu'il n'y a qu'une seule racine?

par **Billball** » 03 Oct 2009, 19:42

Dominique Lefebvre a écrit:Une fonction f présente un extremum (minimum ou maximum) pour chaque point sur lequel sa dérivée f' s'annule. C'est un théorème à savoir. On détermine s'il s'agit d'un max ou d'un min en étudiant sa dérivée seconde f".

non c'est faux, c'est plutôt une tangente horizontale :we:

par **Billball** » 03 Oct 2009, 19:46

choup a écrit:Elle s'annule pour x= racine de 1/3 donc racine de 1/3 est un extremum

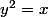
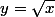
ou

par **Dominique Lefebvre** » 03 Oct 2009, 19:47

Billball a écrit:non c'est faux, c'est plutôt une tangente horizontale :we:

qu'est-ce qui est faux?

par **choup** » 03 Oct 2009, 19:49

Oula je comprends plus très bien! Euh je ne vois qu'une racine je suis bloquée .

par **Billball** » 03 Oct 2009, 19:50

Dominique Lefebvre a écrit:qu'est-ce qui est faux?

f'(x) = 0 f admet une tangente horizontale et pas forcément un minimum ou maximum (c'est la remarque que j'ai pu en tirer de ma colle de vendredi!)

par **choup** » 03 Oct 2009, 19:51

Pour x = - racine de 1/3 elle ne s'annule pas . ???

par **Billball** » 03 Oct 2009, 19:51

choup a écrit:Oula je comprends plus très bien! Euh je ne vois qu'une racine je suis bloquée .

exemple simple :

x² = 1

combien vaut x ??

tu as tjs une racine positive et négative

par **choup** » 03 Oct 2009, 19:52

racine de 1 et - racine de 1 ok

Explication sur les extrema

explication sur les extrema

Qui est en ligne