Bonsoir à vous,
J aimerais démontrer cette propriété rigoureusement mais je ne vois pas trop comment:
Si m et n sont 2 entiers, m divise n ssi vp(m)<=vp(n) pour tous p premier
(Vp(n) est la valuation p-adique de n)
Merci d avance !
Valuation p adique et divisibilité
10 messages
- Page 1 sur 1
Re: Valuation p adique et divisibilité
Bonsoir,
Il y a un sens immédiat. Pour l'autre sens, il faut utiliser le théorème de Gauss.
Il y a un sens immédiat. Pour l'autre sens, il faut utiliser le théorème de Gauss.
Re: Valuation p adique et divisibilité
Bonsoir,
Dans l'autre sens, ne faut-il pas utiliser aussi : si p et q premiers entre eux divisent a, alors p*q divise a ?
Pour une démonstration rigoureuse, il faut utiliser aussi : si p est premier avec q, alors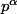 est premier avec
est premier avec 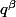 .
.
Dans l'autre sens, ne faut-il pas utiliser aussi : si p et q premiers entre eux divisent a, alors p*q divise a ?
Pour une démonstration rigoureuse, il faut utiliser aussi : si p est premier avec q, alors
Re: Valuation p adique et divisibilité
J'ai chercher un peu plus et j'ai fini par trouver ca
Si m|n alors n=qm donc vp(n)=vp(q)+vp(m) et donc vp(n)>vp(m) pour tout p premier
Si vp(n)>vp(m) pour tout p premier alors on peut écrire
n=p1^a1.....pk^ak et m=p1^b1...pk^bk avec ai>bi pour tout i compris entre 1 et k
On pose gi=ai-bi et c=p1^g1...pr^gr
On a donc n=c*m et donc m|n
D ou l équivalence
Si m|n alors n=qm donc vp(n)=vp(q)+vp(m) et donc vp(n)>vp(m) pour tout p premier
Si vp(n)>vp(m) pour tout p premier alors on peut écrire
n=p1^a1.....pk^ak et m=p1^b1...pk^bk avec ai>bi pour tout i compris entre 1 et k
On pose gi=ai-bi et c=p1^g1...pr^gr
On a donc n=c*m et donc m|n
D ou l équivalence
Re: Valuation p adique et divisibilité
On peut aussi avoir un sens en démontrant Que si vp(m)>Vp(n) alors m ne divise pas n ce qui prouve ainsi que si m|n alors
Vp(m)<=Vp(n)
Et pour avoir l autre sens on dit que si pour tout p premier, vp(m)<vp(n) alors la décomposition en facteurs premiers de m contiendra au moins tous les facteurs premiers de n élevée a une puissance inférieure ou égale et donc Que m|n
Cette demo me paraît moins efficace que la premiere mais bon c'est celle qui m ai venu en premier et elle me paraît bonne
Vp(m)<=Vp(n)
Et pour avoir l autre sens on dit que si pour tout p premier, vp(m)<vp(n) alors la décomposition en facteurs premiers de m contiendra au moins tous les facteurs premiers de n élevée a une puissance inférieure ou égale et donc Que m|n
Cette demo me paraît moins efficace que la premiere mais bon c'est celle qui m ai venu en premier et elle me paraît bonne
Re: Valuation p adique et divisibilité
Bonsoir,
Quelques remarques :
Si tu avais l'inégalité stricte, n serait infini
Ici les n'ont a priori aucune raison d'être tous les mêmes (par exemple m=2 et n=6=2*3). Il vaut mieux écrire
n'ont a priori aucune raison d'être tous les mêmes (par exemple m=2 et n=6=2*3). Il vaut mieux écrire }) et
et }) . Ensuite le raisonnement est le même; il reste juste à dire que le "c" que tu vas obtenir est bien un produit fini de termes.
. Ensuite le raisonnement est le même; il reste juste à dire que le "c" que tu vas obtenir est bien un produit fini de termes.
Peut-être bien, mais généralement, les contraposées sont lourdes, surtout quand le raisonnement direct fait 2 lignes
Ça revient grosso modo au même que ce que tu as dit dans le post d'avant, sauf que ce dernier est mieux formalisé.
Quelques remarques :
Si m|n alors il existe q∈ℕ tel que n=qm, donc vp(n)=vp(q)+vp(m) et donc vp(n)≥vp(m) pour tout p premier.
Si tu avais l'inégalité stricte, n serait infini
Si vp(n)≥vp(m) pour tout p premier, alors on peut écrire
n=p1^a1.....pk^ak et m=p1^b1...pk^bk avec ai>bi pour tout i compris entre 1 et k
On pose gi=ai-bi et c=p1^g1...pr^gr
On a donc n=c*m et donc m|n
Ici les
On peut aussi avoir un sens en démontrant Que si vp(m)>Vp(n) alors m ne divise pas n ce qui prouve ainsi que si m|n alors
Vp(m)<=Vp(n)
Peut-être bien, mais généralement, les contraposées sont lourdes, surtout quand le raisonnement direct fait 2 lignes
Et pour avoir l autre sens on dit que si pour tout p premier, vp(m)<vp(n) alors la décomposition en facteurs premiers de m contiendra au moins tous les facteurs premiers de n élevée a une puissance inférieure ou égale et donc Que m|n
Ça revient grosso modo au même que ce que tu as dit dans le post d'avant, sauf que ce dernier est mieux formalisé.
Re: Valuation p adique et divisibilité
merci pour cette correction c'est sympa 
Par contre je vois pas pourquoi les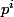 ne peuvent pas être les mêmes
ne peuvent pas être les mêmes
En effet si on pose
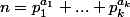
Si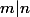 alors on peut écrire
alors on peut écrire
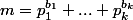 avec
avec
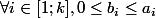
Fin par exemple 3|6, 6=2*3 et 3=2^0*3

Par contre je vois pas pourquoi les
En effet si on pose
Si
Fin par exemple 3|6, 6=2*3 et 3=2^0*3
Re: Valuation p adique et divisibilité
Attention, je n'ai pas dit
J'ai dit
au sens où, pour reprendre mon exemple où je ne considère pas les nombres premiers de valuation nulle
Dans ton écriture tu considères k nombres premiers exactement, alors que les deux nombres n'ont pas forcément tous les deux k facteurs premiers (du moins de valuation non nulle).
Est-ce que ceux que tu considères sont ceux de la décomposition en facteurs premiers de m ? de n ? (dans ce cas il faut le préciser)
C'est pour ça que, pour éviter tous ces tracas, je t'ai suggéré d'écrire le produit de tous les nombres premiers, quitte à ce que certaines valuations soient nulles
lesne peuvent pas être les mêmes
J'ai dit
lespeuvent ne pas être les mêmes (càd où l'un des nombres peut "en avoir plus")
au sens où, pour reprendre mon exemple où je ne considère pas les nombres premiers de valuation nulle
2 = 2^1 et 6 = 2^1 * 3^1
ou un autre exemple pour mieux voir ce que j'insinue
6 = 2^1 * 3^1 et 159120 = 2^4 * 3^2 * 5^1 * 13^1 * 17^1
Dans ton écriture tu considères k nombres premiers exactement, alors que les deux nombres n'ont pas forcément tous les deux k facteurs premiers (du moins de valuation non nulle).
Est-ce que ceux que tu considères sont ceux de la décomposition en facteurs premiers de m ? de n ? (dans ce cas il faut le préciser)
C'est pour ça que, pour éviter tous ces tracas, je t'ai suggéré d'écrire le produit de tous les nombres premiers, quitte à ce que certaines valuations soient nulles
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
