Valuation p-adique et LTE

[LjjMaths]

Bonsoir à tous ! (Je sais pas si cette question est adaptée à cette section du forum mais bon)

Soient a et n deux entiers strictements positifs
Soit p un premier impair tq
a^p congrus à 1 [p^n]
Mq a congrus à 1 [p^(n-1)]

Notons Vp(n) la valuation p-adique de n
Et LTE le theoreme "lifting the exponent"

Voila ce que j'ai FAit mais je bloque :
a^p congrus à 1 [p] donc p ne divise pas a
De plus p ne divise pas 1

Donc d après le theoreme LTE :
Vp(a^p - 1)=Vp(a-1)+Vp(p)=Vp(a-1)+1
Mais après je ne sais plus quoi faire; je pense qu il faut mq Vp(a-1)>=Vp(p^(n-1))
Ce qui permettrait de conclure que
p^(n-1) divisé a-1 et c'est gagné mais je ne sais pas comment faire

je sais que c'est pas des notions courantes au lycée mais bon, merci d avance !!

[Ben314]

Salut,
e sais pas ce que c'est le "LTE" (et si en plus c'est l'acronyme d'un truc en Anglais, c'est encore plus sûr que je sais pas ce que c'est... ).
Sinon, je sais pas trop ce que tu connait concernant les anneaux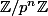 , mais un truc bien connu, c'est que le groupe multiplicatif des inversibles de 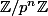est cyclique d'ordre (pour )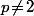
Si on note un entier naturel dont la classe engendre ce groupe alors évidement la classe de ce même dans est un générateur de ce deuxième groupe.
Maintenant, si est un entier, il existe 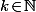tel que 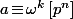et, si 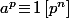, c'est que
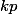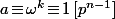Or est générateur de donc d'ordre et signifie en fait que divise donc que divise ce qui assure que vu que est d'ordre )

[LjjMaths]

Salut merci pour cette réponse rapide !
Le theoreme LTE est le suivant
Soit p un nombre premier impaire
Soient a et b deux entiers relatifs distincts et un entier n>=1
Si p divise a-b mais p ne divise ni a ni b
Alors Vp(a^n-b^n)=Vp(a-b)+Vp(n)

J'ai pas du tout compris tout ces Z/pnZ mais je vais essayer de comprendre ! Merci bcp