Valeur Absolue
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 18:39
par minette20 » 06 Déc 2011, 18:39
Bonjour, pourriez-vous me donner un petit coup de pouce s'il vous plaît..
Voici l'exercice :
Soit f la fonction telle que f(x) = (x valeur absolue de x)/x²+1
On note C sa représentation graphique dans le plan muni du repère (O;I;J)
1_ Quel est l'ensemble de définition de la fonction f ?
2.a) Montrer que, pour x>= 0 , f(x) = 1 - 1/x²+1
b) en déduire le sens de variation de la fonction f sur l'intervalle [o; + [
3.a) Montrer que, pour tout réel x, on a f(-x) = -f(x)
b) En déduire que les points M(x;f(x)) et M' (-x;f(-x)) sont symétriques par rapport à O
c) que peut-on en déduire pour C ?
3_ Représenter f sur une calculatrice
Merci d'avance pour votre aide.
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 18:52
par el niala » 06 Déc 2011, 18:52
où bloques-tu ?
la première chose à faire, c'est distinguer les cas x positif et x négatif pour éliminer la valeur absolue
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 18:55
par minette20 » 06 Déc 2011, 18:55
Je sais déjà que l'ensemble de définition de la fonction f est R.
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 18:57
par el niala » 06 Déc 2011, 18:57
OK, passe à la suite, que vaut |x| pour x positif ?
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 19:01
par minette20 » 06 Déc 2011, 19:01
Quand x est positif, la valeur absolue de x vaut " x " non ?
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 19:04
par el niala » 06 Déc 2011, 19:04
bien sûr, tu devrais pouvoir faire le 2a) et même le 2b) en étudiant successivement les sens de variation des fonctions "carré" et "inverse"
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 19:07
par minette20 » 06 Déc 2011, 19:07
D'accord mais en faite c'est pour la question 2.a) Montrer que, pour x>= 0 , f(x) = 1 - 1/x²+1
que je n'y arrive pas.. !
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 19:10
par el niala » 06 Déc 2011, 19:10
allons, allons, tu as pour
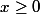
=\frac{x^2}{x^2+1})
tu ne vois pas ce que tu pourrais faire avec
=\frac{x^2+1-1}{x^2+1})
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 19:13
par minette20 » 06 Déc 2011, 19:13
Bah ça fait f(x) = 1 - 1/x²+1 !
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 19:17
par el niala » 06 Déc 2011, 19:17
"bah" aussi, tu peux continuer avec mon indication de 19h04
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 19:40
par minette20 » 06 Déc 2011, 19:40
Sur [0;+00[, la fonction carré donc x² est croissante.
Sur [0;+00[, x²+1 est également croissante.
Sur [0;+00[, 1/x²+1 est décroissante.
Mais après je suis bloquée...
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 19:44
par el niala » 06 Déc 2011, 19:44
dommage, tu y es presque !
1/(x²+1) est décroissante donc -1/(x²+1) est... et donc 1+(-1/(x²+1)) est...
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 20:03
par minette20 » 06 Déc 2011, 20:03
donc -1/(x²+1) est croissante et donc 1+(-1/(x²+1)) est croissante.
Est-ce bien ça ?
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 20:13
par el niala » 06 Déc 2011, 20:13
oui, tu peux continuer
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 20:15
par minette20 » 06 Déc 2011, 20:15
Mais comment montrer que, pour tout réel x, on a f(-x) = -f(x) ... ?
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 20:18
par el niala » 06 Déc 2011, 20:18
tu dois remplacer x par (-x) dans l'expression de f, mais attention
comme tu as travaillé avec x positif, -x est négatif, et dans ce cas, que vaut |-x| ?
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 20:19
par minette20 » 06 Déc 2011, 20:19
Valeur absolue de -x vaut x non ?
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 20:22
par el niala » 06 Déc 2011, 20:22
oui, mais essaie d'en écrire un peu plus à chaque post, sinon ça fait "chat" et pas forum :lol3:
-
minette20
- Membre Naturel
- Messages: 14
- Enregistré le: 06 Déc 2011, 18:37
-
 par minette20 » 06 Déc 2011, 20:25
par minette20 » 06 Déc 2011, 20:25
D'accord, excusez-moi...
Donc si je remplace x par -x dans la fonction f, on a donc :
(-x |-x|)/x²+1.
Soit f(-x) = (-x+x)/x²+1
Donc f(-x)=x²+1
Je pense m'être trompé...
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 06 Déc 2011, 20:39
par el niala » 06 Déc 2011, 20:39
oui, tu as confondu un produit avec une somme,
x|x| c'est x "fois" |x| et non pas x "plus" |x|
que vaut (-x) "fois x ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 190 invités
