salut,
j'ai une petite question : la formule de Moivre est-elle applicable dans le cas d'exposants fractionnaires ?
Une question
17 messages
- Page 1 sur 1
par Quidam » 14 Nov 2006, 12:48
sue a écrit:salut,
j'ai une petite question : la formule de Moivre est-elle applicable dans le cas d'exposants fractionnaires ?
La formule de "De Moivre" est applicable quel que soit l'exposant, entier (positif ou négatif), rationnel, réel et complexe !
[INDENT](Celui qui l'a découverte est Abraham De Moivre, donc en toute rigueur, il faut la mentionner comme "formule de De Moivre". Mais il est vrai que de nombreux auteurs (et professeurs) y font référence par "formule de Moivre" !)[/INDENT]
Elle résulte de la combinaison de la formule :
P.S. Mais il est vrai que je ne me souviens pas l'avoir utilisée avec des puissances autres qu'entières !
par c pi » 14 Nov 2006, 12:58
Bonjour
Voilà un autre point de vue.
Voilà un autre point de vue.
La formule ne s'applique pas à des valeurs rationnelles non entières de z : un tel nombre n = m/p conduirait formellement à :
(cos t - i.sin t)n = (cos t - i.sin t)m/p = [(cos t - i.sin t)m]1/p = (cos mt - i.sin mt)1/p
et cette dernière écriture est illicite car elle tend à exprimer la racine p-ème du nombre complexe cos mt - i.sin mt et on sait qu'un tel nombre n'est pas unique : d'une façon générale, écrire dans l'ensemble C des nombres complexes z = am/p n'a généralement pas de sens. Dans le cas simple de n = 1/3 et a complexe donné l'écriture z = a1/3 conduirait à rechercher z complexe tel que z3 = a. Le cas de a = 1 est édifiant et conduit facilement à trois solutions : les racines cubiques de l'unité, à savoir 1, j = (-1 + i3)/2 et (-1 - i3)/2 = j2. On a 1 + j + j2 = 0
par sue » 14 Nov 2006, 13:15
ok , merci Quidam
mais prenons par exemple l'expression : + isin(\theta))^{\frac{3}{5}})
, normalement avec la formule de De Moivre on a :  + isin(\theta))^{\frac{3}{5}} = cos(\frac{3\theta}{5}) + i sin(\frac{3\theta}{5}))
mais ce qui me dérange c'est quand je pose : +isin(\theta) ) ^{\frac{3}{5}} = cos x + isin x)
et j'essaye de trouver les valeurs de x qui vérifiesnt l'égalité j'obtiens :
en élevant les 2 membres à la puissance 5 il vient :
 +isin(\theta) ) ^3 = (cos x + isin x)^5)
i.e  + isin(3\theta)) = cos 5x + isin 5x)
on doit donc avoir :
d'ou 
soit : + isin(\theta))^{\frac{3}{5}} = cos(\frac{3\theta}{5}+\frac{2k\pi}{5} ) + i sin(\frac{3\theta}{5}+\frac{2k\pi}{5} ))
donc il me semble que l'expression considérée peut prendre 5 valeurs tandis avec la formule de DE Moivre on a une seule valeur ( cas k=0) :doh:
peut-etre je raconte des horreurs mais bon j'aimerais bien que vous m'expliquez :hein:
merci
mais prenons par exemple l'expression :
mais ce qui me dérange c'est quand je pose :
en élevant les 2 membres à la puissance 5 il vient :
on doit donc avoir :
soit :
donc il me semble que l'expression considérée peut prendre 5 valeurs tandis avec la formule de DE Moivre on a une seule valeur ( cas k=0) :doh:
peut-etre je raconte des horreurs mais bon j'aimerais bien que vous m'expliquez :hein:
merci
par sue » 14 Nov 2006, 14:12
j'ai pas encore vu l'exponentielle , mais bon si on peut pas appliquer la formule de DE Moivre dans le cas d'exposant fractionnaire , on peut pas également écrire :
mais est-ce vrai ça ?
par Quidam » 14 Nov 2006, 14:32
Je te remercie c pi d'avoir corrigé mon erreur.
Effectivement, l'expression z^z' a plusieurs significations possibles...
Parmi les réels, on écrit
Mais mon professeur de math' spé m'avait indiqué une définition étendue du logarithme, définition étendue aux nombres négatifs et aux nombres complexes. J'avoue n'avoir quasiment jamais (pour ne pas dire "jamais" tout court) utilisé ce que j'ai appris ce jour là.
On définit ainsi le logarithme d'un complexe par :
Etant donné que
Ainsi, un complexe a une multitude de "logarithmes" et cette multiplicité dans la définition est bien évidemment un lourd obstacle à son utilisation, ce qui explique l'extrême rareté de son emploi !
Mais la définition existe bel et bien !
Il faut que je réfléchisse aux conséquences pour Sue, et il n'est pas exclu que ses difficultés soient directement issues de cette bizarrerie !
Merci en tous cas, de m'avoir rappelé à mes devoirs ! J'avais répondu trop vite !
par c pi » 14 Nov 2006, 14:50
MERCI Quidam de nous faire partager cette extension de la définition du logarithme, il est toujours intéressant d'apprendre... :zen:
par Quidam » 14 Nov 2006, 15:07
Correction :
Effectivement, les soucis de Sue (tiens, c'est joli, ça !) proviennent directement de ta remarque, c pi.
L'expression+i\sin(\theta))^{\frac{3}{5}})
désigne plusieurs complexes différents.
En appliquant la définition du logarithme étendue aux complexes que j'ai donnée dans le post précédent, on peut écrire :
+i\sin(\theta))^{\frac{3}{5}}=e^ { \frac{3}{5}\times \ln(\cos(\theta)+i\sin(\theta))})
Si
on constate que +i\sin(\theta)))
et par conséquent, que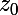 
est bien un des logarithmes de +i\sin(\theta))
.
Les autres logarithmes de sont les nombres complexes : 
Dès lors, l'expression désigne l'un quelconque des nombres )+i\sin( \frac{3}{5}\theta+\frac{6}{5}(k\pi)))
Comme deux valeurs de k distantes d'un multiple de 5 fournissent le même complexe, il n'y a que cinq valeurs différentes.
Donc l'expression désigne cinq nombres différents et +i \sin( \frac{3}{5} \theta))
n'est que l'un d'entre eux ! Il est donc illégal d'écrire :
+i\sin(\theta))^{\frac{3}{5}}=\Large \cos(\frac{3}{5}\theta)+i\sin(\frac{3}{5}\theta))
La conclusion pour Sue, est qu'effectivement, on n'a pas le droit d'utiliser la formule de De moivre pour des exposants non entiers !
Désolé de t'avoir donné une réponse erronée !
Effectivement, les soucis de Sue (tiens, c'est joli, ça !) proviennent directement de ta remarque, c pi.
L'expression
En appliquant la définition du logarithme étendue aux complexes que j'ai donnée dans le post précédent, on peut écrire :
Si
Les autres logarithmes de
Dès lors, l'expression
Comme deux valeurs de k distantes d'un multiple de 5 fournissent le même complexe, il n'y a que cinq valeurs différentes.
Donc l'expression
La conclusion pour Sue, est qu'effectivement, on n'a pas le droit d'utiliser la formule de De moivre pour des exposants non entiers !
Désolé de t'avoir donné une réponse erronée !
encore une question
par sue » 14 Nov 2006, 15:57
merci merci Quidam pour tes explications :jap:
mais là j'ai encore une toute dernière question ( désolée je pose trop de questions :triste: ) .
on a d'aprés la formule d'Euler :
donc
^r = (e^{i\theta})^r)
(1)
et de meme on a tj d'aprés Euler : + i sin(r\theta) = e^{ir\theta})
(2)
or on a^r = e^{ir\theta})
(d'aprés ce j'ai trouvé dans mon livre d'analyse) (3)
donc logiquement on peut conclure d'aprés (1) (2) et (3) que :
: ^r = cos(r\theta) + i sin(r\theta))
, or ce n'est pas le cas pour tt r de Q .
il me semble qu'il y a une contradictrion :mur:
mais là j'ai encore une toute dernière question ( désolée je pose trop de questions :triste: ) .
on a d'aprés la formule d'Euler :
donc
et de meme on a tj d'aprés Euler :
or on a
donc logiquement on peut conclure d'aprés (1) (2) et (3) que :
il me semble qu'il y a une contradictrion :mur:
par maturin » 14 Nov 2006, 16:28
ben ce qu'on a dit précédement tendrait à dire que ^{r})
n'est aps égal à 
mais c'est plutôt égal à 
avec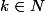 
Mais je t'avoue que c'est surprenant car je n'ai pas mémoire d'être tombé sur ce cas avant et que je me serai facilement gourré.
A croire que dans les exercie sur les complexes on a toujours des puissances de type entier naturel
Mais je t'avoue que c'est surprenant car je n'ai pas mémoire d'être tombé sur ce cas avant et que je me serai facilement gourré.
A croire que dans les exercie sur les complexes on a toujours des puissances de type entier naturel
par sue » 14 Nov 2006, 16:38
ah oui c'est vrai , en fait ce que j'ai trouvé moi c'est : ^r = e^{rx})
pour tt 
mais ici on parle de l'exponentielle complexe donc effectivement n'est pas toujours égale à ^r)
..
un grand merci à vous tous :we:
un grand merci à vous tous :we:
par Quidam » 14 Nov 2006, 20:53
c pi a écrit:MERCI Quidam de nous faire partager cette extension de la définition du logarithme, il est toujours intéressant d'apprendre... :zen:
A ton service !
Je n'ai malheureusement aucune expérience de la nature des calculs engendrés par un tel mouton à cinq pattes !
par crassus » 14 Nov 2006, 22:00
avez vous oublié q'un complexe a 2 racines carrées ? donc que signifie z^1/2 ?
par Quidam » 15 Nov 2006, 08:11
crassus a écrit:avez vous oublié q'un complexe a 2 racines carrées ? donc que signifie z^1/2 ?
Il semble que oui ! Je ne sais pas où j'avais la tête ! J'ai fini par effacer complètement ma première réponse, car c'est une ânerie.
Sue, je pense que tous tes soucis doivent disparaître dès l'instant que tu enregistreras qu'on ne peut pas "élever un complexe" à une puissance autre qu'entière !
Déjà pour x réel positif, on sait qu'il existe deux réels y distincts tels que
On peut d'ailleurs remarquer que si l'écriture
Car il existe q complexes distincts qui, élevés à la puissance p donnent un complexe donné, et (2q) complexes distincts qui, élevés à la puissance 2p donnent ce même complexe. Ainsi
Merci donc à Crassus, d'avoir remis les pendules à l'heure !
par nabot-furtif » 02 Mar 2007, 19:38
bonjour !
simple question... ne peut on pas definir des puissance non entieres de complexes à partir de ça :
a tel que a^p=b ? pN
ainsi a serai la (les) racine(s) "p-ième" de b?
on pourrai alors definir un puissance complexe a^(p/q)?
en fait j'ai pas bien saisi ton dernier post Quidam, concernant le nombre de racine complexes...
dans mon cas, je suis tombé sur le meme probleme...
en effet :
exp(2*i*Pi*a)=(exp(2*i*Pi))^a=1^a=1 avec aQ...
edit : mea culpa, apres 2min de reflexion j'ai compris...
simple question... ne peut on pas definir des puissance non entieres de complexes à partir de ça :
a tel que a^p=b ? pN
ainsi a serai la (les) racine(s) "p-ième" de b?
on pourrai alors definir un puissance complexe a^(p/q)?
en fait j'ai pas bien saisi ton dernier post Quidam, concernant le nombre de racine complexes...
dans mon cas, je suis tombé sur le meme probleme...
en effet :
exp(2*i*Pi*a)=(exp(2*i*Pi))^a=1^a=1 avec aQ...
edit : mea culpa, apres 2min de reflexion j'ai compris...
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : beagle et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :