je voulais savoir si c'était possible de m'expliquer la manière dont il fallait procéder pour calculer f'(0)quel que soit la fonction f(x),j'aimerais comprendre la méthode pour ensuite faire mes exercices.
Je pensais tout d'abord calculer la dérivée de f(x)mais j'en suis vraiment pas sure
Et puis commen lire d'ailleur la dérivée sur un graphique?
Merçi beaucoup a ceux qui se pencheront sur le problème
Une question de dérivation
5 messages
- Page 1 sur 1
Une fonction f est dérivable si la fonction g définie telle que
 = \frac {f(a+h)-f(a)}{h}) Avec
Avec
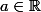 et
et
 admet une limite finie A en 0 ( lorsque h->0 ). On dit alors que f est dérivable en a, et on note f'(a) le nombre derivée de f en a.
admet une limite finie A en 0 ( lorsque h->0 ). On dit alors que f est dérivable en a, et on note f'(a) le nombre derivée de f en a.
Une fonction f est dérivable si et ssi la fonction h définie telle que
 = \frac {f(x)-f(a)}{x-a}) admet une limite finie A en a.
admet une limite finie A en a.
Une fonction f est dérivable si et ssi la fonction h définie telle que
nxthunder a écrit:Une fonction f est dérivable si la fonction g définie telle queAvec
et
admet une limite finie A en 0 ( lorsque h->0 ). On dit alors que f est dérivable en a, et on note f'(a) le nombre derivée de f en a.
Une fonction f est dérivable si et ssi la fonction h définie telle que
admet une limite finie A en a.
Oui mais la en l'occurrence on me donne ma fonction f:x=2x-5
on me demande a quoi est égal f'(0)
je calcule donc la dérivée qui est égale a 2
mais la ou je compren pas c'est qu'aparemen je dois remplacer des x par 0?
et vu qu'il y en a plus...
Je suis vraiment désolé mais j'ai un peu de mal a cerner....
Ta réponse est dans ce que tu as dit :
>>>
je calcule donc la dérivée qui est égale a 2
mais la ou je compren pas c'est qu'aparemen je dois remplacer des x par 0?
et vu qu'il y en a plus...
<<<<
f'(0) = 2 car on
on  = 2) Ainsi que x prenne comme valeur 0, 1.3 , 8933 ou encore 787123131 La dérivée sera toujours égale à 2.
Ainsi que x prenne comme valeur 0, 1.3 , 8933 ou encore 787123131 La dérivée sera toujours égale à 2.
>>>
je calcule donc la dérivée qui est égale a 2
mais la ou je compren pas c'est qu'aparemen je dois remplacer des x par 0?
et vu qu'il y en a plus...
<<<<
f'(0) = 2 car
nxthunder a écrit:Ta réponse est dans ce que tu as dit :
>>>
je calcule donc la dérivée qui est égale a 2
mais la ou je compren pas c'est qu'aparemen je dois remplacer des x par 0?
et vu qu'il y en a plus...
<<<<
f'(0) = 2 caron
Ainsi que x prenne comme valeur 0, 1.3 , 8933 ou encore 787123131 La dérivée sera toujours égale à 2.
merçi infiniment c'est tout de suite plus clair!
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
