Question dérivation 1ère
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 23 Juil 2009, 13:16
par sky-mars » 23 Juil 2009, 13:16
skertel a écrit:
(u*v)'= u'v+v'u
(racine(u))'=u'/(2racine(u))
(uov)'=v'*(u'(v))
(u/v)'=(u'v-v'u)/v² ???
Merci
on va utiliser la formule de la tangente (*)
Soit f(x) = u(x) v(x)
On doit évaluer
-f(x)}{h})
Au numérateur on a :
u(x+h)v(x+h) - u(x)v(x)
Or u(x+h)= u(x) + h u '(x) (*) et v(x+h)= v(x) + h v'(x) (*)
Ce qui nous donne :
(u(x) + h u '(x))( v(x) + h v'(x) ) - u(x)v(x)
on devéloppe :
v'(x) + h( u'(x)v(x) + u(x)v'(x) ))
Ensuite
on reprend notre calcul
-f(x)}{h})
v'(x) + h( u'(x)v(x) + u(x)v'(x) )}{h})
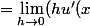v'(x) + u'(x)v(x) + u(x)v'(x) ) = u'(x)v(x) + u(x)v'(x))
d'où le résultat...
pour les autres formules, c'est le même genre de démonstrations
inspire toi de ça pour faire les autres voilà !
-
sky-mars
- Membre Rationnel
- Messages: 542
- Enregistré le: 26 Aoû 2007, 11:27
-
 par sky-mars » 23 Juil 2009, 14:41
par sky-mars » 23 Juil 2009, 14:41
skertel a écrit:
Avec u et v des fonctions déf sur R:
(u*v)'= u'v+v'u (1)
(racine(u))'=u'/(2racine(u))
(uov)'=v'*(u'(v))
(u/v)'=(u'v-v'u)/v² ???
Merci
pose f(x)= u(x)v(x)
utilise la définition du taux d'accroissement:)
ASTUCE : u(x+h)= u(x) + h u' (x)
avec tout ça tu peux me pondre la démonstration (1)
Tu as toutes les cartes en main pour la faire

-
skertel
- Membre Naturel
- Messages: 50
- Enregistré le: 17 Nov 2008, 17:16
-
 par skertel » 26 Juil 2009, 10:39
par skertel » 26 Juil 2009, 10:39
Ok, merci bien, j'ai pu démontrer toutes ces formules ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
