TSTG le premier qui me donne la reponse juste je l'apelle einstein!!!!

[kaz69]

Le benefice realiser par uen entreprise est defini par B(x)=84x-(x^3-30x^2+300X)

a) Quelle doit etre la production x de l'E pour qu elle realise un benef maximal?????

[maturin]

alors pour résoudre cet exercice il faut faire un tableau de variation avec calcul de la dérivée, etude du signe de la dérivée, calcul des valeur aux extremum et limites de l'ensemble de définition, dessin d'un petit tableau pour récapituler tout ça...

fais ces étapes pas par pas et si tu rencontres des difficultés expose nous tes résultats et tes problèmes.
normalement tu devrais pouvoir t'appeler einstein toi meme...

[kaz69]

ba deja jarrive pas a calculer b(x) et la derivé de B(x) car on en a besoin pour faire le tableau de variation
apres coment decomposé mon resultat dans le tableau?

[kaz69]

jpense a voir trouver ce ci est ce que c'est juste s'il te plait?

B(x)=-x^3+30x^2-216x
B'(x)=-3x^2+60x-216

Apres je sais pas comment faire pour rentrer ca dans un tableau de signe et de variation t'as uen idée
merci de ton aide c'est super cool

[maturin]

alors tu as bon pour la dérivée.

Après pour trouver le signe de ta dérivée il faut factoriser B'(x).
B'(x)=-3(x²-20x+72)

par la méthode du discriminant tu vas trouver les racines de x²-60x+72



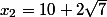
donc B'(x)=-3(x-x1)(x-x2)

tu cherches le signe de x-x1, le signe de x-x2
tu en déduis le signe de B'(x)
tu en déduis les variations de B(x)

tu dois trouver B décroissant pour xx2

le maximum de B est donc soit à la borne d'ouverture de l'ensemble de définition (qui doit être x=0 je pense vu qu'une production ne doit pas pouvoir être négative) soit en x=x2.
Tu calcules les 2 valeurs B(0)=0
B(x2)=136.324

C'est B(x2) le plus grand donc le max est pour x=x2

[kaz69]

merci bcp grace a toi j'ai compris plus de chose et je pourrai le reproduire pour d'autres exercices

J'espere que mon dm sera juste

si tu as msn prend mon adresse
david5569002@hotmail.com

merci encore

[maturin]

ça m'étonne quand même que les racines x1 et x2 soient avec des racines de 7.
vérifie ton énoncé en général les formules données sont souvent prévues pour tomber sur un résultat rond. Mais bon là ça ressemble à de l'économie et les économistes aimen bien les chiffres à virgule.