Trouver les extremums d'une fonction sinus
25 messages
- Page 1 sur 2 - 1, 2
Trouver les extremums d'une fonction sinus
Bonjour, je souhaite trouver le minimum et le maximum de la fonction f(x) = sin2x mais je ne sais pas si mon raisonnement est correcte. Je me demande si on se base uniquement sur la définition de la fonction f(x)=sin x ou s'il y a des calculs à faire. Pourriez-vous me dire si ce que j'ai fait est bon ou pas ? Merci à vous !
On sait que pour étudier une fonction, il faut faire sa dérivée. Ici f(x)=sin2x soit f'(x)= 2cos2x. Il faut donc trouver les points où la dérivée s'annule. Comme cos x s'annule en x =pi/2 +kpi alors ici f'(x) s'annule en 2x= pi/2 +kpi soit x=pi/4 +kpi/2.
On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?
D'où le résultat : le minimum de f(x)=sin2a est 3pi/4 + kpi/2 et le maximum est x=pi/4 +kpi/2.
Est-ce que c'est correcte ? Merci bien
On sait que pour étudier une fonction, il faut faire sa dérivée. Ici f(x)=sin2x soit f'(x)= 2cos2x. Il faut donc trouver les points où la dérivée s'annule. Comme cos x s'annule en x =pi/2 +kpi alors ici f'(x) s'annule en 2x= pi/2 +kpi soit x=pi/4 +kpi/2.
On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?
D'où le résultat : le minimum de f(x)=sin2a est 3pi/4 + kpi/2 et le maximum est x=pi/4 +kpi/2.
Est-ce que c'est correcte ? Merci bien
Re: Trouver les extremums d'une fonction sinus
Bonsoir,
Attention vous mélangez tout. Un maximum est une ordonnée par un abscisse !
Quel est le maximum et le minimum de la fonction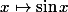 sur
sur  ?
?
Le maximum est la valeur maximale prise par la fonction (ordonnée) et le minimum la valeur minimale prise par la fonction.
Attention vous mélangez tout. Un maximum est une ordonnée par un abscisse !
Quel est le maximum et le minimum de la fonction
Le maximum est la valeur maximale prise par la fonction (ordonnée) et le minimum la valeur minimale prise par la fonction.
Re: Trouver les extremums d'une fonction sinus
La fonction sinus étant 2pi périodique il suffit de l'étudier sur un intervalle d'amplitude 2pi.
Re: Trouver les extremums d'une fonction sinus
Bonsoir Mehdi-128, merci pour votre aide.
La fonction sin x a son maximum à x=pi/2 + 2kpi et son minimum à x=3pi/2 + 2kpi non ?
La fonction sin x a son maximum à x=pi/2 + 2kpi et son minimum à x=3pi/2 + 2kpi non ?
Re: Trouver les extremums d'une fonction sinus
Ok donc c'est au niveau de la période que j'ai faux c'est ça ? Comment passe t-on de pi/4 +kpi/2 à une période de 2pi ? Je suis perdu, désolé si je ne comprends pas...
Re: Trouver les extremums d'une fonction sinus
Ça ne sert à rien de s'embêter avec des 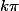 . La fonction sinus est
. La fonction sinus est 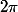 périodique ! Il suffit de l'étudier sur un intervalle d'amplitude
périodique ! Il suffit de l'étudier sur un intervalle d'amplitude 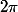 .
.
Considérons la fonction)
Petit exercice : déterminer le maximum et le minimum de .
.
On pourra calculer) et établir le tableau de variation de
et établir le tableau de variation de  .
.
Considérons la fonction
Petit exercice : déterminer le maximum et le minimum de
On pourra calculer
Re: Trouver les extremums d'une fonction sinus
Legolas2mars a écrit:Bonsoir Mehdi-128, merci pour votre aide.
La fonction sin x a son maximum à x=pi/2 + 2kpi et son minimum à x=3pi/2 + 2kpi non ?
Ce passage est juste. Soit
On a en effet :
Et
Re: Trouver les extremums d'une fonction sinus
mehdi-128 a écrit:La fonction sinus étant 2pi périodique il suffit de l'étudier sur un intervalle d'amplitude 2pi.
Effectivement, mais attention dans l'exercice, f est pi-périodique (et c'est la plus petite période de f, mais ce n'est pas demandé...)
Re: Trouver les extremums d'une fonction sinus
hi,
par rapport à ton raisonnement
Tu étudies sin(2x)
Tu dérives : f'
tu trouves x tq f'(x)==0
ces x donnent un minimum local ou maximum local de ta fonction f (aka x->sin(2x))
f'(x)==0 <=> cos(2x)==0
posons X = 2x
cos(X)==0 <=> X = pi/2 ou -pi/2 (modulo 2pi) idem X = pi/2 +kpi
d'où x = (pi/2+kpi)/2
il faut vérifier maintenant que chacun de ces x, injectés dans sin(2x) vérifient soit sin(2x)==1 soit sin(2x)==-1
sin(2*(pi/2+kpi)/2) = sin(pi/2 + kpi)
et effectivement, si k est pair, sin(pi/2 + kpi) vaut 1 sinon -1
j'insiste sur le fait de pas dire que f'(x)==0 hop je trouve un x c'est mon minimum ou maximum (il est juste local).
par ex: essaies de déterminer les min et max de sinc(x)=sin(x)/x
A noter que: on a posé X = 2x pour cos(X)...
autant ne pas s'embêter avec l'étude de fonction et directement considérer sin(X)
par rapport à ton raisonnement
On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?
Tu étudies sin(2x)
Tu dérives : f'
tu trouves x tq f'(x)==0
ces x donnent un minimum local ou maximum local de ta fonction f (aka x->sin(2x))
f'(x)==0 <=> cos(2x)==0
posons X = 2x
cos(X)==0 <=> X = pi/2 ou -pi/2 (modulo 2pi) idem X = pi/2 +kpi
d'où x = (pi/2+kpi)/2
il faut vérifier maintenant que chacun de ces x, injectés dans sin(2x) vérifient soit sin(2x)==1 soit sin(2x)==-1
sin(2*(pi/2+kpi)/2) = sin(pi/2 + kpi)
et effectivement, si k est pair, sin(pi/2 + kpi) vaut 1 sinon -1
j'insiste sur le fait de pas dire que f'(x)==0 hop je trouve un x c'est mon minimum ou maximum (il est juste local).
par ex: essaies de déterminer les min et max de sinc(x)=sin(x)/x
A noter que: on a posé X = 2x pour cos(X)...
autant ne pas s'embêter avec l'étude de fonction et directement considérer sin(X)
la vie est une fête 
Re: Trouver les extremums d'une fonction sinus
mehdi-128 a écrit:Ça ne sert à rien de s'embêter avec des. La fonction sinus est
périodique ! Il suffit de l'étudier sur un intervalle d'amplitude
.
Considérons la fonction
Petit exercice : déterminer le maximum et le minimum de.
On pourra calculeret établir le tableau de variation de
.
C'est ce que j'ai fais, la dérivée de la f(x)=sin2x est bien f'(x)=2cos2x ? Ou j'ai faux aussi ?
C'est au niveau du tableau de variation que je coince, si j'arrive pas à trouver ce qui annule f'(x), comment trouver les maximum et minimum ? Je suis largué, je sais pas comment faire pour étudier la fonction sinus sur l'intervalle (0,2pi)... C'est la première fois que je fais ce genre d'exercice, je suis totalement largué
Re: Trouver les extremums d'une fonction sinus
Attention la période de ) est
est  !
!
En effet :=\sin(2(x+\pi))=\sin(2x+2 \pi) =\sin(2x)=f(x))
On peut étudier sur
sur 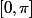 donc
donc 
=0 \Leftrightarrow \cos(2x)=0 \Leftrightarrow (2x=\cdots...))
Je vous laisse finir !
En effet :
On peut étudier
Je vous laisse finir !
Re: Trouver les extremums d'une fonction sinus
Legolas2mars a écrit:mehdi-128 a écrit:Ça ne sert à rien de s'embêter avec des. La fonction sinus est
périodique ! Il suffit de l'étudier sur un intervalle d'amplitude
.
Considérons la fonction
Petit exercice : déterminer le maximum et le minimum de.
On pourra calculeret établir le tableau de variation de
.
C'est ce que j'ai fais, la dérivée de la f(x)=sin2x est bien f'(x)=2cos2x ? Ou j'ai faux aussi ?
C'est au niveau du tableau de variation que je coince, si j'arrive pas à trouver ce qui annule f'(x), comment trouver les maximum et minimum ? Je suis largué, je sais pas comment faire pour étudier la fonction sinus sur l'intervalle (0,2pi)... C'est la première fois que je fais ce genre d'exercice, je suis totalement largué
Le calcul de dérivée est bon, il faut juste déterminer son signe.
En effet, le signe de la dérivée donne les variations de la fonction.
Normalement, le signe d'un cosinus, ça se voit sur un cercle trigonométrique. Tu dois être capable de le déterminer (une petite difficulté étant que c'est cos(2x) et pas cos(x), comme l'ont dit les précédents intervenants)
Re: Trouver les extremums d'une fonction sinus
Dans le 1er message, il y a une phrase (et une seule) qui ne va pas.
"On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?"
Quand tu écris ça, tu démolis tout ton travail :
- tu dis d'une certaine façon que tu t'es trompé dans les lignes précédentes, parce que dans les lignes précédentes, tu as résolu f'(x) = 0, et maintenant tu dis que tu découvres de nouvelles solutions de cette équation f'(x)=0.
C'est bizarre, non ?
En fait tu dis que tu avais déjà tous les nombres de la forme Pi/4+kPi/2. Et maintenant tu ajoutes les nombres de la forme 3Pi/4+kPi/2.
Tu ne remarques rien sur ces 2 séries de nombres ? Tu es sur que ces 2 séries de nombres sont différentes ?
Tu supprimes dons cette phrase de ta première réponse, tu reformules un petit peu, et c'est bon.
"On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?"
Quand tu écris ça, tu démolis tout ton travail :
- tu dis d'une certaine façon que tu t'es trompé dans les lignes précédentes, parce que dans les lignes précédentes, tu as résolu f'(x) = 0, et maintenant tu dis que tu découvres de nouvelles solutions de cette équation f'(x)=0.
C'est bizarre, non ?
En fait tu dis que tu avais déjà tous les nombres de la forme Pi/4+kPi/2. Et maintenant tu ajoutes les nombres de la forme 3Pi/4+kPi/2.
Tu ne remarques rien sur ces 2 séries de nombres ? Tu es sur que ces 2 séries de nombres sont différentes ?
Tu supprimes dons cette phrase de ta première réponse, tu reformules un petit peu, et c'est bon.
Re: Trouver les extremums d'une fonction sinus
Ok merci pour votre aide !!
Alors je crois avoir cibler une de mes erreurs.
Quand on fait f'(x)=0, on a 2cos2x=0 soit cos2x=0. Là ce que je faisais c'est que je cherchais à résoudre une équation du type cos a = cos b (c'est ce que je vous ai posté dans mon premier poste), donc cos 2x= cos (pi/2)
alors 2x=(pi/2)+2kpi et 2x=-(pi/2)+2kpi, ce qui est FAUX (merci fatal_error).
Ce qu'il faut donc faire (dites moi si c'est bon) c'est : cos2x=0 soit cos X = 0 avec X=pi/2+kpi ou X=-pi/2+kpi (et non 2kpi ! car cos (x) s'annule pour x=pi/2+kpi).
Donc : X=2x=pi/2+kpi ou 2x=-pi/2+kpi
Soit : x=pi/4+kpi/2 ou x=-pi/4+kpi/2
On remplace dans sin(2x) pour voir si cela respecte -1 et 1.
sin(2x) = sin( 2. (pi/4+kpi/2)) = sin (pi/2+kpi)
sin(2x) = sin (2. (-pi/4+kpi/2)) = sin (-pi/2+kpi)
Donc si k=0, sin (pi/2+kpi)= sin (pi/2)=1 et sin (-pi/2+kpi)=sin (-pi/2) = - sin (pi/2) = sin(3pi/2)= -1.
Du coup le minimum de sin2x est x=3pi/2+kpi et le maximum est x=pi/2+kpi.
C'est bien ça ? Merci
Alors je crois avoir cibler une de mes erreurs.
Quand on fait f'(x)=0, on a 2cos2x=0 soit cos2x=0. Là ce que je faisais c'est que je cherchais à résoudre une équation du type cos a = cos b (c'est ce que je vous ai posté dans mon premier poste), donc cos 2x= cos (pi/2)
alors 2x=(pi/2)+2kpi et 2x=-(pi/2)+2kpi, ce qui est FAUX (merci fatal_error).
Ce qu'il faut donc faire (dites moi si c'est bon) c'est : cos2x=0 soit cos X = 0 avec X=pi/2+kpi ou X=-pi/2+kpi (et non 2kpi ! car cos (x) s'annule pour x=pi/2+kpi).
Donc : X=2x=pi/2+kpi ou 2x=-pi/2+kpi
Soit : x=pi/4+kpi/2 ou x=-pi/4+kpi/2
On remplace dans sin(2x) pour voir si cela respecte -1 et 1.
sin(2x) = sin( 2. (pi/4+kpi/2)) = sin (pi/2+kpi)
sin(2x) = sin (2. (-pi/4+kpi/2)) = sin (-pi/2+kpi)
Donc si k=0, sin (pi/2+kpi)= sin (pi/2)=1 et sin (-pi/2+kpi)=sin (-pi/2) = - sin (pi/2) = sin(3pi/2)= -1.
Du coup le minimum de sin2x est x=3pi/2+kpi et le maximum est x=pi/2+kpi.
C'est bien ça ? Merci
Re: Trouver les extremums d'une fonction sinus
Je cite la conclusion : le minimum de sin2x est x=3pi/2+kpi et le maximum est x=pi/2+kpi.
Le maximum serait donc atteint quand x=pi/2+kpi. C'est à dire par exemple, pour k=1, ça donne x = 3 pi/2.
Tiens ? 3pi/2 est donc un maximum, et il était aussi un minimum.
Relis mon précédent message (celui de 12h09). Tu étais proche de la solution dans ton 1er message, et depuis mehdi-128 t'a emmené vers des trucs complètement faux.
Le maximum serait donc atteint quand x=pi/2+kpi. C'est à dire par exemple, pour k=1, ça donne x = 3 pi/2.
Tiens ? 3pi/2 est donc un maximum, et il était aussi un minimum.
Relis mon précédent message (celui de 12h09). Tu étais proche de la solution dans ton 1er message, et depuis mehdi-128 t'a emmené vers des trucs complètement faux.
Re: Trouver les extremums d'une fonction sinus
Le plus simple serait de tracer le graphe de la fonction ) ce qui n’est pas compliqué si on connaît le graphe du sinus
ce qui n’est pas compliqué si on connaît le graphe du sinus
Re: Trouver les extremums d'une fonction sinus
lyceen95 a écrit:Dans le 1er message, il y a une phrase (et une seule) qui ne va pas.
"On sait par définition que la fonction sin x admet un maximum à x=pi/2 + 2kpi et un minimum à x=3pi/2 + 2kpi. Donc ici, f'(x) s'annule aussi en 3pi/4 + kpi/2 ?"
Quand tu écris ça, tu démolis tout ton travail :
- tu dis d'une certaine façon que tu t'es trompé dans les lignes précédentes, parce que dans les lignes précédentes, tu as résolu f'(x) = 0, et maintenant tu dis que tu découvres de nouvelles solutions de cette équation f'(x)=0.
C'est bizarre, non ?
En fait tu dis que tu avais déjà tous les nombres de la forme Pi/4+kPi/2. Et maintenant tu ajoutes les nombres de la forme 3Pi/4+kPi/2.
Tu ne remarques rien sur ces 2 séries de nombres ? Tu es sur que ces 2 séries de nombres sont différentes ?
Tu supprimes dons cette phrase de ta première réponse, tu reformules un petit peu, et c'est bon.
Oui c'est vrai Lyceen95, ça ne peut pas être à la fois le maximum et le minimum. Je n'avais pas vérifié pour k=1...
Donc quand on obtient : x=pi/4+kpi/2 ou x=-pi/4+kpi/2, il ne faut pas les insérer dans sin(2x) ??
Donc si je reviens à mon premier poste, on a bien pour la fonction sin(x) :
sin (pi/2 + 2kpi)= 1
sin (3pi/2 + 2kpi) = -1
Pour la fonction sin(2x) on fait comment puisque c'est ce que j'ai fais juste avant et c'est faux...
Re: Trouver les extremums d'une fonction sinus
Je sais faire la courbe de sin (x) mais pas de sin(2x).
C'est simple, je me base sur quelques points comme sin(0)=1 (passe par l'origine), sin(pi/2)= 1, sin (pi)=0 et sin (3pi/2)= -1. Impossible de placer sin (2x), je sais pas ce que ça représente.
C'est simple, je me base sur quelques points comme sin(0)=1 (passe par l'origine), sin(pi/2)= 1, sin (pi)=0 et sin (3pi/2)= -1. Impossible de placer sin (2x), je sais pas ce que ça représente.
Re: Trouver les extremums d'une fonction sinus
Si tu prends des valeurs spéciales de ) tout en sachant qu’elle est π-périodique, on devine que c’est la même courbe que le sinus mais un peu plus « écrasée »
tout en sachant qu’elle est π-périodique, on devine que c’est la même courbe que le sinus mais un peu plus « écrasée »
Re: Trouver les extremums d'une fonction sinus
Legolas2mars a écrit:Je sais faire la courbe de sin (x) mais pas de sin(2x).
C'est simple, je me base sur quelques points comme sin(0)=1 (passe par l'origine), sin(pi/2)= 1, sin (pi)=0 et sin (3pi/2)= -1. Impossible de placer sin (2x), je sais pas ce que ça représente.
Il suffit de prendre quelques points pour voir l'allure. Posons
On a fait une période, il suffit de faire une translation de vecteur
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
