Bonjour,
Je possède uniquement la relation U(n+1) d'une suite.
U(n+1)= ((U(n)/n)*0.6)+U(n)
Est-il possible de trouver Un-1 à l'aide uniquement de Un+1?
J'ai beau chercher, je n'arrive pas à trouver comment retourner l'équation...
Toute aide est la bienvenue,
Merci!
Trouver U(n-1) à l'aide de U(n+1)
14 messages
- Page 1 sur 1
 Trouver U(n-1) à l'aide de U(n+1)
Trouver U(n-1) à l'aide de U(n+1)
Modifié en dernier par Gaelv le 06 Nov 2018, 15:59, modifié 1 fois.
Re: Trouver U(n-1) à l'aide de U(n+1)
bonjour,
d'abord corrige ton problème de parenthèse
est ce ou
ou 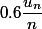 ?
?
d'abord corrige ton problème de parenthèse
est ce
Modifié en dernier par mathelot le 06 Nov 2018, 15:54, modifié 1 fois.
Re: Trouver U(n-1) à l'aide de U(n+1)
U(n+1)= U(n)/n*0.6+U(n)
là, tu as Un+1=f(n,Un)
tu cherches quoi exactement ?
PS ! mets des parenthèses, on ne peut rien faire sans savoir ce qui est au dénominateur
là, tu as Un+1=f(n,Un)
tu cherches quoi exactement ?
PS ! mets des parenthèses, on ne peut rien faire sans savoir ce qui est au dénominateur
Re: Trouver U(n-1) à l'aide de U(n+1)
Gaelv a écrit:Bonjour,
Je possède uniquement la relation U(n+1) d'une suite.
ça ne serait pas plutôt
U(n+1)= U(n)/n*0.6+U(n-1)
Est-il possible de trouver Un-1 à l'aide uniquement de Un+1?
J'ai beau chercher, je n'arrive pas à trouver comment retourner l'équation...
Toute aide est la bienvenue,
Merci!
Modifié en dernier par mathelot le 06 Nov 2018, 15:57, modifié 1 fois.
Re: Trouver U(n-1) à l'aide de U(n+1)
Si c'est U(n+1) = Un ( 1 + 0.6/n) = Un * an
Un = U(n+1) / an et U(n-1) = Un / a (n-1)
U (n-1) = U(n+1) / (an * a(n-1))
Un = U(n+1) / an et U(n-1) = Un / a (n-1)
U (n-1) = U(n+1) / (an * a(n-1))
Re: Trouver U(n-1) à l'aide de U(n+1)
mathelot a écrit:Gaelv a écrit:Bonjour,
Je possède uniquement la relation U(n+1) d'une suite.
ça ne serait pas plutôt
U(n+1)= ((U(n)/n)*0.6)+U(n-1)
Est-il possible de trouver Un-1 à l'aide uniquement de Un+1?
J'ai beau chercher, je n'arrive pas à trouver comment retourner l'équation...
Toute aide est la bienvenue,
Merci!
Non il s'agit bien de U(n+1)= ((U(n)/n)*0.6)+U(n)
Re: Trouver U(n-1) à l'aide de U(n+1)
Merci de votre aide, j'ai corrigé les parenthèse!
A quoi correspond a nodgim?
A quoi correspond a nodgim?
Re: Trouver U(n-1) à l'aide de U(n+1)
Du coup si on utilise que U(n) et n dans l'équation, ça donne:
U(n-1) = ( ((U(n)/n)*0,6)+U(n) ) / ( (1+(0,6/n)) * (1+(0,6/(n+1))) )
J'ai peut-être mal compris comment intégrer a à l'équation car la formule ci-dessus ne fonctionne pas
U(n-1) = ( ((U(n)/n)*0,6)+U(n) ) / ( (1+(0,6/n)) * (1+(0,6/(n+1))) )
J'ai peut-être mal compris comment intégrer a à l'équation car la formule ci-dessus ne fonctionne pas
Re: Trouver U(n-1) à l'aide de U(n+1)
"U(n+1)= ((U(n)/n)*0.6)+U(n)
= U(n) * (1+ 0.6/n)
Est-il possible de trouver Un-1 à l'aide uniquement de Un+1?
"
donc
U(n+1) = U(n-1)* (1+ 0.6/n)* (1+ 0.6/(n-1))
soit
U(n-1) = U(n+1) / [(1+ 0.6/n)* (1+ 0.6/(n-1))]
= U(n) * (1+ 0.6/n)
Est-il possible de trouver Un-1 à l'aide uniquement de Un+1?
"
donc
U(n+1) = U(n-1)* (1+ 0.6/n)* (1+ 0.6/(n-1))
soit
U(n-1) = U(n+1) / [(1+ 0.6/n)* (1+ 0.6/(n-1))]
Re: Trouver U(n-1) à l'aide de U(n+1)
Bon reprenons.
On a
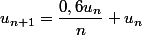
On commence par mettre u_n en facteur pour y voir plus clair
\qquad\qquad\qquad(\star))
C'est une relation de récurrence entre et
et  .
.
On peut donc l'écrire entre et
et 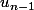 : il suffit de remplacer partout n par n-1. On a ainsi
: il suffit de remplacer partout n par n-1. On a ainsi
)
Il n'y a plus qu'à remplacer u_n par cette valeur dans) :
:
\Big(\dfrac{0,6 }{n}+1\Big))
Après pour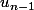 fonction de
fonction de  il 'y a plus qu'à diviser.
il 'y a plus qu'à diviser.
Ce mécanisme est général : si tu as l'expression de u_{n+1} en fonction de u_n, tu peux donc avoir l'expression de u_n en fonction de u_{n-1}, ou de u_{n-1} en fonction de u_{n-2}, ou etc. : c'est le principe d'une relation de récurrence "on détermine un terme en fonction de son précédent". Après il n'y a plus qu'à remplacer (éventuellement en cascade).
On a
On commence par mettre u_n en facteur pour y voir plus clair
C'est une relation de récurrence entre
On peut donc l'écrire entre
Il n'y a plus qu'à remplacer u_n par cette valeur dans
Après pour
Ce mécanisme est général : si tu as l'expression de u_{n+1} en fonction de u_n, tu peux donc avoir l'expression de u_n en fonction de u_{n-1}, ou de u_{n-1} en fonction de u_{n-2}, ou etc. : c'est le principe d'une relation de récurrence "on détermine un terme en fonction de son précédent". Après il n'y a plus qu'à remplacer (éventuellement en cascade).
Modifié en dernier par hdci le 06 Nov 2018, 17:32, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Trouver U(n-1) à l'aide de U(n+1)
Ah ben le temps que j'écrive tout cela, pascal16 avait donné la réponse...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Trouver U(n-1) à l'aide de U(n+1)
le post de Nodgin donnait la démarche bien avant moi
J'ai juste trouvé une façon de l'écrire sans utiliser Latex que je trouve très lente (plus lent que l'éditeur d'équation sous office/libre office/open office).
J'ai juste trouvé une façon de l'écrire sans utiliser Latex que je trouve très lente (plus lent que l'éditeur d'équation sous office/libre office/open office).
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

