[Exercice] - Trinome et triangles

par **El Tyranos** » 10 Déc 2006, 18:22

Bonjour, j'ai un soucis avec un exercice, je n'arrive pas a progresser car je suis bloqué, voici le sujet :

Les triangles équilateraux T1 et T2, d'aire respectives S1 et S2 ont un pérmiètre total constant L. Quelle est la plus petite aire totale possible (S1+S2) des deux triangles T1 et T2 ?

Voici la ou j'en suis :

Soit x la longeur d'un coté du triangle S1
Soit y la longeur d'un coté du triangle S2

L=3y+3x
y=-x+(L/3)

Je suis maintenant bloqué, quelqu'un pourrait-il de donner un coup de main ?

Merci !

par **Elsa_toup** » 10 Déc 2006, 18:38

Bonjour,

Il faut maintenant que tu exprimes S1+S2 en fonction de x et y...

par **El Tyranos** » 10 Déc 2006, 19:20

S1=x²*(racine3/4)
S2=y²*(racine3/4)

S1+S2=x²*(racine3/4)+y²*(racine3/4)
S1+S2=x²*(racine3/4)+(-x+(L/3))²*(racine3/4)
S1+S2=x²*(racine3/4)+((-x)²+2*x*(L/3)+(L/3)²*(racine3/4)
S1+S2=x²*(racine3/4)+(x²+(2Lx/3)+(L²/9))*(racine3/4)

Et re-blocage :s

par **Elsa_toup** » 10 Déc 2006, 19:38

Oui, alors en regroupant les termes, on a donc que:
S1+S2 =

.

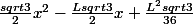
C'est pas joli-joli, mais c'est un trinôme du second degré.
Donc c'est dérivable en x, et ça a un minimum...

Je te laisse te casser la tête dessus ! :lol4:

par **El Tyranos** » 10 Déc 2006, 19:43

Oui j'ai pensé au trinome mais je n'arrivais pas a réduire, merci pour le coup de pouce je m'y remet.

par **El Tyranos** » 10 Déc 2006, 19:56

Argh il y avait une erreur dans mes calculs que j'ai corrigée,
S1+S2=x²*(racine3/4)+(x²+(2Lx/3)+(L²/9))*(racine3/4)

j'essaye de mettre ca sous forme de trinôme.

PS : comment affiche tu des images avec les fractions, les racines etc ?

par **Elsa_toup** » 10 Déc 2006, 20:02

Ah pardon, je n'avais pas relu très attentivement ton résultat.
J'utilise les balises TEX au-dessus, et ce site : http://fr.wikipedia.org/wiki/Wikip%C3%A9dia:Formules_TeX

Typiquement, pour aller vite, la fraction A sur B s'écrit : \frac{A}{B} et tu surlignes cette expression et cliques sur TEX.

Je te conseille vivement de prévisualiser ton message avant de l'envoyer, pour vérifier... :we:

par **El Tyranos** » 10 Déc 2006, 20:41

Voilà je trouve ce trinome.

Son minimum est

J'isole L et je trouve

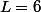
Après on developpe S1+S2(6)

Je continue de chercher il faut trouver x :marteau:

par **Elsa_toup** » 10 Déc 2006, 21:08

Je ne comprends pas ce que tu fais.
Moi j'ai dérivé le trinome et j'ai trouvé que la fonction est décroissante puis croissante, et que le minimum est atteint en L/6....
Donc après il n'y a plus qu'à calculer f(L/6) si on veut connaître cette aire minimale (mais je crois que ce n'est même pas nécessaire).

par **El Tyranos** » 10 Déc 2006, 21:28

Oui petite erreur de ma part !

D'où, la plus petite aire totale possible (S1+S2) est

par **El Tyranos** » 10 Déc 2006, 21:30

Je pense que ce resultat est correct ^^
Merci beaucoup Elsa ! :++:

par **Elsa_toup** » 10 Déc 2006, 21:30

Pas de quoi :we:

[Exercice] - Trinome et triangles

[Exercice] - Trinome et triangles

Qui est en ligne