Trigonometrie... angles associés
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 14:24
par biwou » 07 Mar 2007, 14:24
Bonjour a tous ,
voila j'ai un exercice a faire pendant les vaccances et je n'arrive pas a trouver !!
merci de m'apporté de l'aide ^^!!
En utilisant les angles associés , démontrer que :
cos²(pi/8)+cos²(3pi/8)+cos²(5pi/8)+cos²(7pi/8) = 2
MErci de l'aide
BIWOU... :we:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 14:37
par amine801 » 07 Mar 2007, 14:37
slt
voila des formules tres utiles pour ton exo ca sera une des deux premiere
au choix
=\sin(x)\\<br />$\cos(x+\frac{\pi}{2})=-\sin(x) \\<br />$\cos (x+\pi)=-\cos (x) \\<br />$\sin (x+\pi)=-\sin (x)\\<br />$\cos (\pi-x)=-\cos (x) \\<br />$\sin (\pi-x)=\sin (x)\\<br />$\cos(-x)=\cos(x)\\<br />$\sin(-x)=-\sin(x) \\<br />$\cos(x+\frac{\pi}{2})=-\sin(x) \\<br />$\sin(x+\frac{\pi}{2})=\cos(x) \\<br />$\sin(\frac{\pi}{2}-x)=\cos(x) \\<br /><br />$\cos 2a= \cos^2 a-\sin^2 a \\<br />$\sin 2a= 2\cos a\sin a)
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 14:41
par biwou » 07 Mar 2007, 14:41
amine801 a écrit:slt
voila des formules tres utiles pour ton exo ca sera une des deux premiere
au choix
=\sin(x)\\<br />$\cos(x+\frac{\pi}{2})=-\sin(x) \\<br />$\cos (x+\pi)=-\cos (x) \\<br />$\sin (x+\pi)=-\sin (x)\\<br />$\cos (\pi-x)=-\cos (x) \\<br />$\sin (\pi-x)=\sin (x)\\<br />$\cos(-x)=\cos(x)\\<br />$\sin(-x)=-\sin(x) \\<br />$\cos(x+\frac{\pi}{2})=-\sin(x) \\<br />$\sin(x+\frac{\pi}{2})=\cos(x) \\<br />$\sin(\frac{\pi}{2}-x)=\cos(x) \\<br /><br />$\cos 2a= \cos^2 a-\sin^2 a \\<br />$\sin 2a= 2\cos a\sin a)
Merci pour les formules , je les connais je els ai deja !! mais j'arrive aps avoir comment les utilisés: faut que je multiplie par 4 pour mettre sur le denomionateur de 8 c sa ?
jai fait un devellope ment est j'ai trouvé un truc comme 2+ cos (8pi/4) !!
merci de l'aide ^^
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 15:02
par amine801 » 07 Mar 2007, 15:02
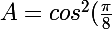+cos^2(\frac{3\pi}{8})+cos^2( \frac{5\pi}{8})<br />+cos^2(\frac{7\pi}{8})\\<br />=cos^2(\frac{\pi}{8})+cos^2(\frac{3\pi}{8})+cos^2(\frac{\pi}{2}+\frac{\pi}{8})<br />cos^2(\frac{\pi}{2}+\frac{3\pi}{8}))
en utilisant la formule (2)
on a
=(-sin(\frac{\pi}{8}))^2=sin^2(\frac{\pi}{8}))
=(-sin(\frac{3\pi}{8}))^2=sin^2(\frac{3\pi}{8}))
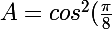+cos^2(\frac{3\pi}{8})+sin^2(\frac{\pi}{8})+sin^2(\frac{3\pi}{8}))
et mnt avec la formule
+sin^2(x)=1)
on a
A=2
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 15:08
par biwou » 07 Mar 2007, 15:08
ah ok merci beaucoup ^^
poiur ton aide
je vais faire les autres plus facilement maintenant... :we:
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 16:37
par biwou » 07 Mar 2007, 16:37
Je bloque comment on fait quand on a :
* sin(\frac{\pi}{8}) + cos(\frac{25\pi}{8}) * sin(\frac{11\pi}{8})) = 1)
Merci de la nouvelle aide... ^^
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 16:49
par amine801 » 07 Mar 2007, 16:49
les fonctions cos sin sont periodique alors
=cos(\frac{25\pi}{8}-4\pi)=cos(\frac{\pi}{8}))
=sin(\frac{11\pi}{8}-2\pi)=sin(\frac{3\pi}{8}))
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 16:52
par amine801 » 07 Mar 2007, 16:52
les fonctions cos sin sont periodique alors
et en utilisant les formules si dessus alors
=cos(\frac{25\pi}{8}-3\pi)=-cos(\frac{\pi}{8}))
=sin(\frac{11\pi}{8}-\pi)=-sin(\frac{3\pi}{8}))
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 17:02
par biwou » 07 Mar 2007, 17:02
amine801 a écrit:les fonctions cos sin sont periodique alors
et en utilisant les formules si dessus alors
=cos(\frac{25\pi}{8}-3\pi)=-cos(\frac{\pi}{8}))
=sin(\frac{11\pi}{8}-\pi)=-sin(\frac{3\pi}{8}))
j'arrive a trouver un truc du genre : cos (pi/8)
----------
sin (pi/8)
c sa !! ?
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 17:09
par amine801 » 07 Mar 2007, 17:09
hein :doh: soit plus claire apres tu doit utilser la formule
=sin a cos b+sin b cos a)
:we:
-
biwou
- Membre Relatif
- Messages: 101
- Enregistré le: 29 Nov 2006, 15:04
-
 par biwou » 07 Mar 2007, 17:30
par biwou » 07 Mar 2007, 17:30
amine801 a écrit:hein :doh: soit plus claire apres tu doit utilser la formule
=sin a cos b+sin b cos a)
:we:
dsl mais jarrive pas a trouvé 1 mais jtrouve 2... ? :triste:
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 07 Mar 2007, 17:42
par amine801 » 07 Mar 2007, 17:42
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
