Trigo
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 27 Déc 2006, 18:02
par math* » 27 Déc 2006, 18:02
Bonsoir,
j'ai un petit problème avec la consigne de l'exercice :
Tout d'abord, on a S=1+cosx+cos2x+...+cosnx
et S'=sinx+sin2x+...+sin(nx)
On a
ix}}{1-e^{ix}})
(problème de suite évidemment)
Et la deuxième question c'est : "factoriser
x}{2}})
au numérateur..
Quelqu'un peut-il m'expliquer ce qu'il faut faire sans me donner la réponse ? merci.
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 27 Déc 2006, 18:43
par math* » 27 Déc 2006, 18:43
Personne ne peut m'expliquer ce que signifie factoriser au numérateur ?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 27 Déc 2006, 18:56
par anima » 27 Déc 2006, 18:56
math* a écrit:Personne ne peut m'expliquer ce que signifie factoriser au numérateur ?
Je t'aurai bien aidé si j'avais vu les exponentielles appliquées aux complexes. Je sais vaguement que ca te donne des sinus; donc tu utilise les formules, tu retourne en nombres "normaux", et tu factorise :we:
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 27 Déc 2006, 19:01
par math* » 27 Déc 2006, 19:01
:doh: Po compris.
Le truc des expos c'est bon j'maîtrise. :zen:
Nan mais sérieusement, le truc qui me paraît bizarre c'est qu'on me dit de factoriser quelque chose au numérateur, qui n'est pas au numérateur !!
Alors est-ce que ça veut dire qu'il faut que je transforme le num pour arriver à mettre en évidence la forme que l'on me donne ?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 27 Déc 2006, 19:06
par anima » 27 Déc 2006, 19:06
math* a écrit::doh: Po compris.
Le truc des expos c'est bon j'maîtrise. :zen:
Nan mais sérieusement, le truc qui me paraît bizarre c'est qu'on me dit de factoriser quelque chose au numérateur, qui n'est pas au numérateur !!
Alors est-ce que ça veut dire qu'il faut que je transforme le num pour arriver à mettre en évidence la forme que l'on me donne ?
Bravo, sherlock :zen:
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 27 Déc 2006, 19:09
par math* » 27 Déc 2006, 19:09
lol. je sens le f... de g...! :ptdr:
Bon ben je vais allé essayé de voir ça alors. merci anima.
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 27 Déc 2006, 19:13
par anima » 27 Déc 2006, 19:13
math* a écrit:lol. je sens le f... de g...! :ptdr:
Bon ben je vais allé essayé de voir ça alors. merci anima.
Ne me prends pas au sérieux, surtout. Il n'y avait aucun foutage de geule la-dedans (surtout qu'en plus, je n'ai jamais fait ce genre d'expo) :we:
-
math*
- Membre Rationnel
- Messages: 544
- Enregistré le: 04 Déc 2006, 17:05
-
 par math* » 27 Déc 2006, 19:17
par math* » 27 Déc 2006, 19:17
Nan nan ne t'inquiète pas je disais ça pour rire !
-
sue
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 10 Oct 2006, 20:33
-
 par sue » 27 Déc 2006, 22:55
par sue » 27 Déc 2006, 22:55
salut,
il s'agit de ''factorier le numérateur
par }{2}})
"
} =)
}{2}} \left(e^{-ix\frac{(n+1)}{2}}-e^{ix\frac{(n+1)}{2}}\right))
mtn il suffit d'utiliser Euler...
j'imagine que tu cherche à déterminer S et S' , si oui tu peux factoriser le dénominateur par

.
sinon voilà deux formules efficaces pour ce genre de problèmes :

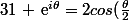 e^{i\frac{\theta}{2})
et
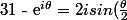 e^{i\frac{\theta}{2})
donc pour ton exo il suffit d'appliquer directement la 2ème formules puis simplifier.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
