Triangles - Géométrie

[ATRM]

Bonjour,

Voici le système que j'étudie :



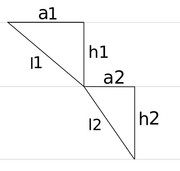
Sachant que je connais h1 et h2, et que je fixe a1+a2, est-il possible de trouver l1 et l2 (ou l1+l2) ?

Je ne sais pas si c'est une question lycée ou autre ... Désolé si la catégorie n'est pas la bonne !

Merci d'avance

[GaBuZoMeu]

Quatre inconnues (a1, a2, l1, l2), trois équations (deux fois Pythagore et la valeur de a1+a2) : ça ne va pas le faire !

[ATRM]

Je ne sais pas si cela servira mais ...
les angles A1 (oppsé à a1) et A2 (opposé à a2) sont reliés par la relation de Snell-Descartes :
sinA1/V1 = sinA2/V2
où V1 et V2 sont connues.

[GaBuZoMeu]

Cachottier, va !
Il est évident que cette information est indispensable : elle nous fournit la quatrième équation qui manquait. Je te laisse écrire ces quatre équations (il faut bien que tu travailles un peu, n'est-ce pas ?).

Tu as un exercice de détermination de plus court chemin d'un point dans un milieu à un autre point dans un autre milieu, les deux milieux étant séparés par une frontière rectiligne, c'est ça ?

[ATRM]

Mon problème peut en effet se rapporter à ça (c'est un peu plus compliqué mais j'ai essayé de simplifier au plus possible pour le poster ici)
il ne s'agit cependant pas de chercher le plus court chemin, mais la longueur du chemin (c'est un unique chemin puisque si l'angle A1 change, le point d'arrivée sera différent, les propriétés des deux milieux étant fixes).

Donc j'ai les quatres équations :

(1) : l1² = a1² + h1² (h1 connu)
(2) : l2² = a2² + h2² (h2 connu)
(3) : a1 + a2 = delta (delta connu)
(4) : sinA1 = (V1/V2) sinA2 = a1 / l1 (V1/V2 connu)

[LB2]

Bonjour,

Si on détermine le plus court chemin, ce sera assez facile de calculer sa longueur, non?

[GaBuZoMeu]

Le plus court n'est sans doute pas le bon terme, disons le plus rapide.

Maintenant que les quatre équations sont là, il n'y a plus qu'à les résoudre.

[ATRM]

Encore une fois, je tiens à préciser qu'il n'y a qu'un seul chemin possible !
Les vitesses de propagation dans les deux milieux étant fixes, l'angle d'incidence qui permet d'atteindre le point B depuis le point A (tous les deux fixes aussi) est unique !!!

[GaBuZoMeu]

Non, il n'y a pas qu'un seul chemin ! Mais il y a un seul chemin à temps de parcours minimal et, selon le principe de Fermat, c'est le chemin optique.
Et alors, la résolution des équations, ça progresse ?

[ATRM]

Serais-tu en train de me dire qu'un rayon partant du point A pourrait arriver en B avec plusieurs angle d'incidence ?

Et bien ça tourne en rond T.T .......
Je ne suis définitivement pas un as du calcul....
Surtout qu'après j'aimerais ne pas me limiter à deux milieux, mais à N milieux...

[LB2]

Ce que GBZM veut dire, c'est qu'il y a une unique solution au système formé par tes 4 équations.
Tu peux commencer par mettre l'équation (4) au carré et à procéder par subsitution.

[GaBuZoMeu]

Serais-tu en train de me dire qu'un rayon partant du point A pourrait arriver en B avec plusieurs angle d'incidence ?

Non. Si tu me lisais bien, tu verrais que j'écris que le rayon suit le chemin qui a le plus court temps de parcours parmi tous les chemins possibles, et que ce chemin est unique.