On considere la fonction f(x)=3x^3-2000 definie sur [0,10]
1)Apres avoir fait l'étude necessaire,tracer le tableau de variation de f
2)Combien y a t il de solution(s) a l'equation f(x)=0? Justifier soigneusement la réponse
3) En précisant la methode , determiner une valeur approche au centieme pr;)s de la (des) solution(s)
une entreprise va fabriquer des millions de brique de jus de fruit en carton Elle doivent se présenter sous la forme de pavés droit a base carré et de hauteur égale a 3 fois le coté de la base .Le volume desire est de 2litre
Afin de faire le reglage des machines, on a besoin de determiner les dimensions de ces briques au dixieme de milimetre pr;)s
4) Montrer que l'étude précedente permet de résoudre le probleme
Merci de repondre vite car je suis totalement perdu
Travail non compris
4 messages
- Page 1 sur 1
petitmecdu44 a écrit:On considere la fonction f(x)=3x^3-2000 definie sur [0,10]
1)Apres avoir fait l'étude necessaire,tracer le tableau de variation de f
2)Combien y a t il de solution(s) a l'equation f(x)=0? Justifier soigneusement la réponse
3) En précisant la methode , determiner une valeur approche au centieme pr;)s de la (des) solution(s)
une entreprise va fabriquer des millions de brique de jus de fruit en carton Elle doivent se présenter sous la forme de pavés droit a base carré et de hauteur égale a 3 fois le coté de la base .Le volume desire est de 2litre
Afin de faire le reglage des machines, on a besoin de determiner les dimensions de ces briques au dixieme de milimetre pr;)s
4) Montrer que l'étude précedente permet de résoudre le probleme
Merci de repondre vite car je suis totalement perdu
En quelle classe êtes vous ?
bonjour,
=9x^2)
f'>0 sauf en un point.
f est strictement croissante sur
=0 \Leftrightarrow x^3=\frac{2000}{3} \Leftright x = 10 \sqrt[3] {\frac{2}{3}})
la racine appartient à ]8;9[ car f(8)f(9)<0
Pour des valeurs approchées, faire tourner à la calculette
une méthode de Newton via la formule de récurrence
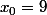

elle donne des valeurs approchées de la racine du polynome.
d'autre part, le calculateur Wolfram alpha est ton ami.
f'>0 sauf en un point.
f est strictement croissante sur
la racine appartient à ]8;9[ car f(8)f(9)<0
Pour des valeurs approchées, faire tourner à la calculette
une méthode de Newton via la formule de récurrence
elle donne des valeurs approchées de la racine du polynome.
d'autre part, le calculateur Wolfram alpha est ton ami.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
