DM Terminale S sur les suites

[Ziler26]

Bonjour à tous, j'ai un Dm à rendre, et je bloque sur le 3ème exercice de celui-ci à partir de la fin de la question c),et j'aimerais votre aide pour comprendre d'où vient mon problème. Voici l'énoncé:

Soit la suite (un) définie pour n appartient N, par: Un=2+3(1/4)^n

a) Etudier la monotonie de la suite (Un).
b) Déterminer, si elle existe, la limite la suite (Un) quand n tend vers +00
c) On considère l'algorithme ci-dessous.

variables

u et s sont des nombres réels
k et n sont des entiers naturels

Initialisation

Lire la valeur de n
S prend la valeur 0

Traitement

Pour k variant de 0 à n

u prend la valeur 2+3(1/4)^k

s prend la valeur s+u

Fin de pour

Sortie

Afficher s

Quel sera le résultat affiché en sortie si on choisit n=2?
Si on choisit n=3?

Plus gènèralement, que permet de calculer cet algo pour un entier naturel n choisi?

d) On appelle Sn, la valeur de S affichée en sortie en fonction du n choisi. Exprime Sn en fonction de n.
En déduire si elle existe, la limite la suite (Sn) quand n tend vers +00.

e) Plus génèralement, on considère une suite de réels (Un) et la suite (Sn) définie par Sn=u0 + u1 +u2+....un
Indiquer pour chaque proposition suivante si elle est vraie ou fausse en justifiant.
Proposition 1: Si la suite Un est convergente, alors la suite (Sn) l'est aussi.
Proposition 2: Les suites (Un) et (Sn) ont même sens de variation.

Voici maintenant mes réponses trouvées:

a) On étudie le signe de Un+1/Un
Un+1/Un= (2+3(1/4)^n+1)/(2+3(1/4)^n)
=(1/4)^(n+1-n)
=1/4<1
Donc la suite est décroissante

b) Un=2+3(1/4)^n
2 tend vers 2
n tend vers +00

3 tend vers 3
n tend vers +00

(1/4)^n tend vers 0
n tend vers +00

Par produit:
lim 3(1/4)^n=0
n tend vers +00

Par somme:
lim 2+3(1/4)^n=2+0=2
n tend vers +00

lim(Un)=2
n tend vers +00

c) Si on choisit n=2, on obtient S=3
Si on choisit n=3, on obtient 4 en sortie

Cet algo permet de calculer pour tout n choisi la somme de termes consécutifs Sn somme des (n+1) premiers termes de la suite Un (c'est la que je pense avoir faux, car en calculant à la main je ne trouve pas la même chose qu'en programmant)

d) Sn= 1+2 +3 (1/4) + 2 +3 (1/4)² + .....+2+3(1/4)^n (ici aussi, surtout si c'est faux précédemment, par extension ça l'est là aussi)

Je vous remercie d'avance pour vos réponses

[SpiderPapouN]

Bonjour Ziler26.

Voici maintenant mes réponses trouvées:

a) On étudie le signe de Un+1/Un

non ,tu veux comparer ce quotient à 1, encore faut - il que tu aies au préalable prouvé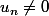 pour tout entier naturel ...

Un+1/Un= (2+3(1/4)^n+1)/(2+3(1/4)^n)
=(1/4)^(n+1-n)

Comment obtiens - tu une telle simplification ?????? par ???? sauf que c'est absolument faux, sauf pour de très rares cas particuliers inintéressants... donc ton calcul est faux. Et si tu étudiais le signe de ?

b)
lim(Un)=2
n tend vers +00

Oui, c'est ok.

c) Si on choisit n=2, on obtient S=3
Si on choisit n=3, on obtient 4 en sortie

Je ne pense pas vu que le premier terme de la suite est 5...et que les termes sont strictement positifs.

Cet algo permet de calculer pour tout n choisi la somme de termes consécutifs Sn somme des (n+1) premiers termes de la suite Un (c'est la que je pense avoir faux, car en calculant à la main je ne trouve pas la même chose qu'en programmant)

[/quote]

Bah non, c'est ça, ce sont les calculs qui sont faux.

[pascal16]

Je pense tes démarches justes, mais l'explication est calamiteuse.

a) On étudie le signe de Un+1/Un
Un+1/Un= (2+3(1/4)^n+1)/(2+3(1/4)^n)
=(1/4)^(n+1-n)
On n'a pas le droit d'enlever le "+2" et le calcul est faux
(Un+1)-Un est plus facile à calculer car "2" s'en va et tu met 3(1/4)^n en facteur


b) Un=2+3(1/4)^n
Gagne du temps et de l’efficacité, le minimum de choses justes suffit :

(1/4)^n tend vers 0
n tend vers +00 (suite géométrique de raison <1 en valeur absolue)

Par produit:
lim 3(1/4)^n=0
n tend vers +00

Par somme :
lim 2+3(1/4)^n=2+0=2
n tend vers +00

conclusion : ....

[pascal16]

Un=2+3(1/4)^n

Uo=2+3(1/4)^0 = 2+3*1 = 5
U1= 2+3(1/4)^1 = 2 + 3/4 =11/4
U2 = 2+3(1/4)^2 = 2+ 3/16 =35/16
...

soit So=5, S1 = 31/4, S2 = 159/16...

[Ziler26]

Ok, c'est bien ce qu'il me semblait pour la question a) merci de ta réponse, je vais pouvoir corriger ça et faire la suite

[Ziler26]

A la d) je n arrive pas du tout a trouver la limite de sn car j ai beau chercher, un n est ni arithmétique ni géométrique vu qu a un+1-un je trouve 33(1/4)^n. Du coup je me demande si en fait elle n a pas de limite
et pour la question e), à la prop 2, j'ai déclaré qu'elle était fausse car l'une est décroissante et l'autre croissante, mais je ne suis pas sur que cela soit une justification correcte?