Terminal ES dm

par **titine** » 13 Nov 2012, 08:45

Commençons par l'exercice 2 :

MathsProbleme a écrit:EXERCICE 2:
1)Soit f la fonction définie sur [0;10]par: f(x)=x^3-15x²+75x
a)Faire afficher la représentation graphique de la fonction f sur un écran de calculatrice.

Fait ?

b)Déterminer f'(x) et f''(x).

Tu ne sioas pas calculer la dérivée d'une fonction polynôme ?

c)Déterminer le sens de variation de la fonction f' puis son signe sur [0;10].

Pour étudier le sens de variation de la fonction f' il faut étudier le signe de sa dérivée c'est à dire f''.

par **Anonyme** » 13 Nov 2012, 08:48

MathsProbleme a écrit:

L'énoncé explique que

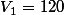
et que

car le volume (exprimé en litre) perd 75% pendant la semaine et on ajoute 120 litres

A toi de rédiger une démo par récurrence sur l'indice

1) via une phase initialisation
c'est à dire une "vérification" que cette relation est vraie pour l'indice

2) et via une phase d'hérédité
c'est à dire : il faut démontrer que si cette relation est vraie à l'indice

alors cette relation est vraie à l'indice

par **titine** » 13 Nov 2012, 08:58

ptitnoir a écrit:L'énoncé explique que
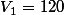
et que ( car le volume (exprimé en litre) perd 75% pendant la semaine et on ajoute 120 litres )

A toi de rédiger une démo par récurrence sur n
via une phase initialisation ( n=1 )
et via une phase d'hérédité ( si c'est vrai à l'indice n alors il faut démontrer que c'est vrai à l'indice n+1 )

Je ne pense pas qu'une récurrence soit nécessaire (ni que le raisonnement par récurrence soit au programme de TES ...)
Je pense que rédiger correctement le raisonnement :

( car le volume (exprimé en litre) perd 75% pendant la semaine et on ajoute 120 litres )

suffit.

par **Anonyme** » 13 Nov 2012, 09:02

@titine
Oui tu as raison
Désolé pour cette erreur

par **titine** » 13 Nov 2012, 09:09

MathsProbleme je crois que tu aurais intérêt à ouvrir 2 fils différents pour chacun de tes exercices. Ça serait plus clair.

par **MathsProbleme** » 13 Nov 2012, 12:35

titine a écrit:Commençons par l'exercice 2 :

Fait ?

Tu ne sioas pas calculer la dérivée d'une fonction polynôme ?

Pour étudier le sens de variation de la fonction f' il faut étudier le signe de sa dérivée c'est à dire f''.

Si j'ai réussi a trouver les dérives et c'est tout. Peut tu me dire comment il faut commencer pour étudier le signe de f''stp

par **MathsProbleme** » 13 Nov 2012, 12:38

titine a écrit:MathsProbleme je crois que tu aurais intérêt à ouvrir 2 fils différents pour chacun de tes exercices. Ça serait plus clair.

Oui c'est vrai je n'y ai pas pensé. Est ce que il y a des choses sur lesquel tu pourrais m'aider ?

par **MathsProbleme** » 13 Nov 2012, 12:39

ptitnoir a écrit:L'énoncé explique que
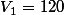
et que
car le volume (exprimé en litre) perd 75% pendant la semaine et on ajoute 120 litres

A toi de rédiger une démo par récurrence sur l'indice
1) via une phase initialisation
c'est à dire une "vérification" que cette relation est vraie pour l'indice

2) et via une phase d'hérédité
c'est à dire : il faut démontrer que si cette relation est vraie à l'indice alors cette relation est vraie à l'indice

Nous n'avons jamais parler d'une phase d'hérédité ni de verification

par **MathsProbleme** » 13 Nov 2012, 12:41

titine a écrit:Je ne pense pas qu'une récurrence soit nécessaire (ni que le raisonnement par récurrence soit au programme de TES ...)
Je pense que rédiger correctement le raisonnement :

suffit.

Merci ,il s'agit bien de la première question ?

par **MathsProbleme** » 13 Nov 2012, 13:44

titine a écrit:Je parle de

Pour l'autre exo, utilise un autre fil.

Est ce fait ? Oui-Non.

Qu'est ce que tu trouves pour f'(x) et pour f'(x) ?

Oui j'ai trouvé f'(x)=3x^2-30x+75
f''(x)= 6x-30
Ce sont les seuls choses que j'ai trouvé

par **titine** » 13 Nov 2012, 13:52

MathsProbleme a écrit:Oui j'ai trouvé f'(x)=3x^2-30x+75
f''(x)= 6x-30
Ce sont les seuls choses que j'ai trouvé

Signe de f''(x)= 6x-30 :
On a 6x - 30 > 0 (c'est à dire positif)
lorsque 6x > 30
x > 5
Donc sur [5 ; 10] f''(x) positif donc f' croissante
Et sur [0 ; 5] f''(x) négatif donc f' décroissante.
Trace le tableau de variations de f'.
f' a un minimum. Calcule ce minimum.
Que peux tu alors en déduire pour le signe de f'(x) ?
Et donc que peux tu en déduire pour f ?

par **MathsProbleme** » 13 Nov 2012, 14:02

titine a écrit:Signe de f''(x)= 6x-30 :
On a 6x - 30 > 0 (c'est à dire positif)
lorsque 6x > 30
x > 5
Donc sur [5 ; 10] f''(x) positif donc f' croissante
Et sur [0 ; 5] f''(x) négatif donc f' décroissante.
Trace le tableau de variations de f'.
f' a un minimum. Calcule ce minimum.
Que peux tu alors en déduire pour le signe de f'(x) ?
Et donc que peux tu en déduire pour f ?

Ah d'accord merci et pour trouver le minimum il faut faire comment ?

par **titine** » 13 Nov 2012, 16:23

Oh ! Tu fais un petit effort de réflexion !

Tu as tracé le tableau de variations de f'.
Elle est décroissante puis croissante.
Donc elle atteint son minimum quand x = ...
Et ce minimum est f'(...) = ...

par **Anonyme** » 13 Nov 2012, 16:43

@MathsProbleme

IMPORTANT A RETENIR :

Ce qu'il faut comprendre c'est que la représentation graphique d'une fonction

du second degré
comme la fonction définie par

avec a,b et c 3 nombres donnés tels que

est une parabole dont le sommet est le point d'abscisse

ET ce point

de coordonnées (

) (qui est appelé "sommet" de la parabole)
représente :
- soit LA valeur minimale pour la fonction

si

- soit LA valeur maximale pour la fonction

si

ps1)
Il n'est pas nécessaire de tracer cette parabole
car on peut déduire cette propriété en "lisant" le tableau de variation de la fonction f

ps2)
Dans cette exercice la fonction

qui est du second degré est la fonction dérivée....

par **MathsProbleme** » 13 Nov 2012, 17:28

titine a écrit:Oh ! Tu fais un petit effort de réflexion !

Tu as tracé le tableau de variations de f'.
Elle est décroissante puis croissante.
Donc elle atteint son minimum quand x = ...
Et ce minimum est f'(...) = ...

Oui mais je sais pas comment on fait fin j'ai juste besoin que tu me donne la méthode

par **Anonyme** » 13 Nov 2012, 18:03

@MathsProbleme

Si on augmente de

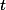
un nombre

connu , on obtient après augmentation le nombre

Par exemple de l'argent placé dans une banque à un taux 2,25%

Une "annuité" veut dire que ton argent rapporte 2,25% après 1 an

ps1)
Et si on diminue de

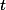
un nombre

connu , on obtient après diminution le nombre

ps2)

ou

sont appelés des coefficients multiplicateurs

et si on augmente successivement un nombre

de

suivi de

alors on obtient le nombre

ps3)
QUESTION :
Si tu as compris alors essaie de calculer le taux de diminution qui résulte d'une augmentation de 10% suivie d'une diminution de 10%

par **titine** » 13 Nov 2012, 18:43

MathsProbleme a écrit:Oui mais je sais pas comment on fait fin j'ai juste besoin que tu me donne la méthode

Je ne comprends pas ce que tu veux dire ...

Je reprends :

Tu as tracé le tableau de variations de f'.

est ce fait ?

Elle est décroissante sur [0 ; 5] puis croissante sur [5 ; 10].
Donc elle atteint son minimum quand x = ?

par **MathsProbleme** » 13 Nov 2012, 18:48

titine a écrit:Je ne comprends pas ce que tu veux dire ...

Je reprends :
est ce fait ?

Oui c'est fait le tableau,je sai pas je n'arrive pas

par **MathsProbleme** » 13 Nov 2012, 18:49

titine a écrit:Je ne comprends pas ce que tu veux dire ...

Je reprends :
est ce fait ?

Le tableau j'ai fait,mais je n'arrive pas a voir comment il faut faire pour trouver le minimum

par **titine** » 13 Nov 2012, 19:06

Tu te fiches de moi ?
Elle est décroissante sur [0 ; 5] puis croissante sur [5 ; 10].
Tu as donc une flèche qui descend de x=0 à x=5, puis une flèche qui monte de x=5 à x=10.
Le point le plus bas sera atteint quand x = ?

Terminal ES dm

Qui est en ligne