Devoirs maison terminal

[macha]

Bonjour,
je n'arrive pas a trouver les réponses de ce Dm... si vous pouviez m'aider merci :ptdr:
Un artisan fabrique entre 10 et 40 bijoux fantaisie par jour. Le coût journalier de fabrication, en euro, de x bijoux est donnée par la fontion c definie sur [10;40] par c(x)=x^2-20+175.
Partie 1
1. Calculer c'(x), puis etudier son signe.
J'ai trouvé c'(x)= 2x-20 mais pas le tableau de signe.
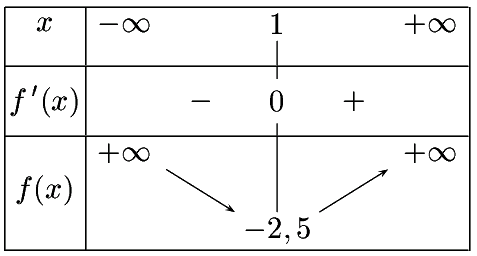
2. En deduire le tableau de variation de la fonction c. :hein:

partie 2
Les bijoux sont vendus 20€. On suppose qu'ils sont tous vendu.
1. r(x)=20x
a.exprimer le benefice b(x) en fonction de x.
b. Calculr le benefice b(x) pour chacune des valeurs de x suivantes; 10, 20 et 30
c. Après avoir calculé b'(x) déterminer la valeur de x réalisant le benefice maximal et donner ce benefice.

Voila, je suis bloquer a la question 1 merci pour aide :++:

[kelthuzad]

Salut,

Avant toute chose est-ce que t'as fonction serait plutôt ?

[macha]

Oui c'est tout a fait sa ! (Je n'arrive pas a ecrire le carré)

[siger]

Bonjour

Si c'(x) = 2(x-10) de quel tableau de signe s'agit-il?

c'>0 si x>10 ne necessite pas un tableau qui n'est utile que dans le cas de produits ou de divisions de polynomes......

[macha]

Etudier le signe ne signifie pas qu'il faut faire un tableau ? (je suis perdu dans ce chapitre ...)

[siger]

Re

Pas forcement!
exemples:
1-
signe de (2x-3) on trouve que (2x-3)>0 si x>3/2 ce qui est suffisant et necessite pas de tableau (ce serait un tableau sans interet, a une seule ligne)
2-
(2x-3)(x+2)
on connait (2x-3)>0 si x> 2/3
mais il faut maintenant determiner le signe de x+2
x+2 >0 si x>-2
Il FAUT maintenant faire un tableau de signe pour combiner les deux resultats ce qui conduit a
(X+2)(2x-3) <0 si -2

[macha]

Je comprend pas d'ou viennent tous c'est chiffre alors que c'(x)=2x-20...

[siger]

Re

j'ai malheureusement essayé de t'expliquer avec des exemples a quoi servait un tableau de signes!!!!!

[kelthuzad]

C'était un exemple pour que tu vois que le tableau de signe n'est nécessaire que pour des cas plus complexes. La dérivée est bien 2x - 20 qui s'annule quand x = 10. Si x est plus petit que 10 on voit que c'(x) est négatif donc c est décroissant. Quand x est plus grand que 10 c'(x) est positif donc c croissant.

[macha]

D'accords je comprend mieux merci

[kelthuzad]

Tu peux t'inspirer de ce tableau trouvé sur google image.



Tu es dans le même cas.
- En haut ce n'est pas 1 mais 10 car pour toi c'(10) = 0
- C'est bien sûr c et pas f
- Ce n'est pas -2,5. Si tu veux trouver pour ta valeur il faut calculer c(10) = 10² - 20*10 + 175 = ...

[macha]

Merci beaucoup

[macha]

Je bloque dans la deuxième partie a la question 2d si vous pouvier m'aider une derniere fois merci :)

[kelthuzad]

Il n'y a pas de question 2d lol

[macha]

C pardon :)

[macha]

T peux m'aider a la c alors ? :)

[kelthuzad]

Salut,

J'ai besoin de faire les premières questions pour y arriver. Donc le bénéfice c'est le prix de vente moins le cout de fabrication.





euros


euros


euros



On résout -2x+40 = 0
x = 20
Cela veut dire qu'il y a un changement de monotonie de b en x = 20. (La fonction était croissante et devient décroissante ou l'inverse...)
Pour savoir dans quel sens :
On voit que b'(x) est positif quand x 20, b'(x) est négatif donc b est décroissante quand x > 20.
La valeur maximale de b(x) sur [10,40] (définie sur cet intervalle) est donc
euros

[macha]

Merci beaucoup tout me parait bon mais je ne comprend pas comment vous avez trouver b'(x) ? Moi j'ai trouver 2x simplement :hein:

[kelthuzad]

Re,



Pour dériver un terme qui comprend une somme on dérive les termes un par un. Autrement dit la dérivée de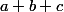 c'est

Lorsqu'on a un facteur (comme -1) il reste où il est, dérivée de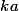 est avec k un nombre quelconque.

La dérivée de est donc

La dérivée de est 40 car la dérivée de est 1.

La dérivée d'un nombre (de -175 ici) est 0.

Donc la dérivée est

PS : pourquoi quand je mets [tex ]-2x[/tex ] il m'écrit f(x)=x² lol

[macha]

Merci beaucoup et une petite question en plus qui n'est pas sur ce devoir, la dérivé de f(x)=x+16+(256/x) ? Merci apres c'est bon :)