Tangentes Communes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
RejaneCRDn
- Messages: 9
- Enregistré le: 05 Oct 2016, 17:52
-
 par RejaneCRDn » 24 Oct 2016, 18:17
par RejaneCRDn » 24 Oct 2016, 18:17
Bonjour,
J'ai un exercice sur les tangentes communes à deux paraboles.
Voici l'énoncé :
Déterminer les tangents communes aux deux paraboles P1 et P2 d'équations respectives

Je commence alors par calculer la dérivée de l'équation appartenant à P1 que j'ai appelé f. On a donc
=2x)
Ensuite je calcule la tangente à P1 en un point quelconque et j'obtiens

Je fais de meme avec La parabole P2.
J'ai donc
=-2x+8)
Et

Ensuite je sais qu'il faut que je fasse un système mais je ne sais pas sous quel forme le faire. Pouvez m'aider svp.
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 24 Oct 2016, 18:52
par danyL » 24 Oct 2016, 18:52
bonsoir
à mon avis (à confirmer) il faut mettre les équations de droite sous la forme T1 = c1 x + d1 et T2 = c2 x + d2
si les droites sont les memes elles ont le meme coefficient directeur et meme ordonnée à l'origine
Modifié en dernier par
danyL le 24 Oct 2016, 18:57, modifié 1 fois.

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 24 Oct 2016, 18:56
par laetidom » 24 Oct 2016, 18:56
Bonsoir,
J'ai trouvé ça :

- iii95907JPG.JPG (25.97 Kio) Vu 439 fois
moi, j'ai mis a = b et obtiens :
2a = 8 - 2b ==> a = b = 2
-
RejaneCRDn
- Messages: 9
- Enregistré le: 05 Oct 2016, 17:52
-
 par RejaneCRDn » 24 Oct 2016, 19:00
par RejaneCRDn » 24 Oct 2016, 19:00
laetidom a écrit:Bonsoir,
J'ai trouvé ça :
iii95907JPG.JPG
moi, j'ai mis a = b et obtiens :
2a = 8 - 2b ==> a = b = 2
Merci de votre réponse mais Je ne comprends pourquoi vous avez fait cela? Pouvez m'expliquer.
De plus les tangentes que vous trouvez sont parallèles mais elles ne sont pas communes aux deux paraboles.

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 24 Oct 2016, 19:05
par laetidom » 24 Oct 2016, 19:05
ah oui communes, je regarde ! . . .
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 24 Oct 2016, 19:06
par siger » 24 Oct 2016, 19:06
bonsoir
deux possibilites:
a-comme tu as fait
il faut que les deux droitesT1 et T2 soient confondues, donc elles doivent avoir des coefficients egaux
2a = -2b+8
-a^2 = b^2 - 14
ce qui conduit a a+b = 8 et ab = 25( sauf erreur) donc a une equation du second degre
b -
ecrire que la droite T2 coupe la premiere parabole en un point double( delta=0)
...'...
-
RejaneCRDn
- Messages: 9
- Enregistré le: 05 Oct 2016, 17:52
-
 par RejaneCRDn » 24 Oct 2016, 19:11
par RejaneCRDn » 24 Oct 2016, 19:11
danyL a écrit:bonsoir
à mon avis (à confirmer) il faut mettre les équations de droite sous la forme T1 = c1 x + d1 et T2 = c2 x + d2
si les droites sont les memes elles ont le meme coefficient directeur et meme ordonnée à l'origine
Merci de votre réponse.
Une fois que j'ai fais ce que vous me dites je trouve :

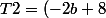*x+b^2-14)
Cela nous fait :

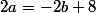
Etes vous d'accord avec cela ?
Si oui, il faut développer le système mais dois je mettre la deuxième ligne du système au carré pour pour remplacer les inconnus par ce que je connais ?
-
RejaneCRDn
- Messages: 9
- Enregistré le: 05 Oct 2016, 17:52
-
 par RejaneCRDn » 24 Oct 2016, 19:13
par RejaneCRDn » 24 Oct 2016, 19:13
siger a écrit:bonsoir
deux possibilites:
a-comme tu as fait
il faut que les deux droitesT1 et T2 soient confondues, donc elles doivent avoir des coefficients egaux
2a = -2b+8
-a^2 = b^2 - 14
ce qui conduit a a+b = 8 et ab = 25( sauf erreur) donc a une equation du second degre
b -
ecrire que la droite T2 coupe la premiere parabole en un point double( delta=0)
...'...
Merci pour la réponse, je vais continuer sur la première méthode, je vais faire cela demain. Je vous dirais ce que je trouve !
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 24 Oct 2016, 19:17
par danyL » 24 Oct 2016, 19:17
dans la premiere equation tu peux substituer a par sa valeur en fonction de b
tu obtiens une équation du 2nd degré à résoudre
ou comme l'a fait siger plus élégamment avec la somme et le produit des racines
une fois les racines b1 et b2 trouvées, dans l'équation de la tangente tu remplaces b par b1 et a par (-b1 + 4)
cela donne une droite
puis de meme en remplaçant b par b2, tu obtiens une autre droite
sur le graphique qu'a fait laetidom tu peux vérifier si les résultats sont cohérents
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 24 Oct 2016, 19:41
par Razes » 24 Oct 2016, 19:41
C'est juste, tu peut continuer pour déterminer les points
)
et
)
Résous le système :


- Courbe.jpg (32.81 Kio) Vu 394 fois
Clique sur la courbe pour l’agrandir.
-
RejaneCRDn
- Messages: 9
- Enregistré le: 05 Oct 2016, 17:52
-
 par RejaneCRDn » 24 Oct 2016, 21:17
par RejaneCRDn » 24 Oct 2016, 21:17
Razes a écrit:C'est juste, tu peut continuer pour déterminer les points
)
et
)
Résous le système :

Courbe.jpg
Clique sur la courbe pour l’agrandir.
Merci beaucoup, j'ai trouvé la même chose que vous !
Si cela ne vous dérange pas j'ai un autre exercice sur le quel j'ai du mal. Je l'ai mis sur le forum aujourd'hui sous le nom de "problème d'optimisation". Merci d'avance
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 24 Oct 2016, 21:44
par Razes » 24 Oct 2016, 21:44
Tu as trouvé quoi comme points A, B, C et D?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
