Tangentes communes à deux cercles

[Archytas]

Je voudrais connaitre la méthodes pour trouver les équations des 4 tangentes communes au cercle trigonométrique et au cercle d'équation (x-5)²+(y-3)²=1, ça m'avait l'air simple et erreur de calcul ou de méthode je n'arrive pas à trouver :(. Quelqun pourrait m'eclaircir ?!

PS: j'ai essayé en utilisant le fais que les droites auront forcément pour vecteurs normaux du centre des cercles et qu'elles admettent exactement un unique couble (x;y) par cercle dans les systèmes. j'ai pensé qu'il y aurait assez de condition pour arriver aux solutions mais je ne trouve quand même pas !

[Lostounet]

Je voudrais connaitre la méthodes pour trouver les équations des 4 tangentes communes au cercle trigonométrique et au cercle d'équation (x-5)²+(y-3)²=1, ça m'avait l'air simple et erreur de calcul ou de méthode je n'arrive pas à trouver . Quelqun pourrait m'eclaircir ?!

PS: j'ai essayé en utilisant le fais que les droites auront forcément pour vecteurs normaux du centre des cercles et qu'elles admettent exactement un unique couble (x;y) par cercle dans les systèmes. j'ai pensé qu'il y aurait assez de condition pour arriver aux solutions mais je ne trouve quand même pas !

Salut,

Si tu veux une méthode bidon, voici comment je procède. Je ne suis pas tout à fait sûr...

Tout droite du plan non parallèle aux axes a pour équation réduite quelque chose de la forme (comment je sais qu'elles sont pas parallèles aux axes, bah on regarde les cercles, on conjecture etc...) :

y = mx + p

En partant de la définition d'une tangente, on sait que celle ci doit couper le cercle en un seul point, ce qui veut dire que le système suivant doit avoir une solution unique:


x^2 + y^2 = 1
y = mx + p

En remplaçant y par mx + p dans la première équation, on aboutit à l'équation de degré 2 suivante:


(1 + m²)x² + (2mp)x + (p² - 1) = 0

Or cette équation ne doit pas avoir plus d'une solution, donc on impose au discriminant d'être nul, et on lie m et p par la relation suivante:

4m²p² - 4(1 + m²)(p² - 1) = 0


Ce qui peut se simplifier un peu:

p = +-;)(m² + 1)



On fait ensuite pareil pour l'autre cercle, en exprimant l'unicité de la solution en fonction de m et de p:
Un peu plus lourd:

(-10 + 2mp - 6m)² - 4(1 + m²)(24 - 6p + p²) = 0


En substituant p, on se ramène à une équation assez élaborée (j'ai pris p>0)


(-10 + 2m;)(m² + 1) - 6m)² - 4(1 + m²)(24 - 6;)(m² + 1) + (m² + 1)) = 0


On trouve deux solutions, et je pense que pour p< 0 on en trouve 2 autres.
T'as tes 4? tangentes... hum (j'ai pas trop regardé)


A vérifier...

[chan79]

Salut,

Si tu veux une méthode bidon, voici comment je procède. Je ne suis pas tout à fait sûr...

Tout droite du plan non parallèle aux axes a pour équation réduite quelque chose de la forme (comment je sais qu'elles sont pas parallèles aux axes, bah on regarde les cercles, on conjecture etc...) :

y = mx + p

En partant de la définition d'une tangente, on sait que celle ci doit couper le cercle en un seul point, ce qui veut dire que le système suivant doit avoir une solution unique:


x^2 + y^2 = 1
y = mx + p

En remplaçant y par mx + p dans la première équation, on aboutit à l'équation de degré 2 suivante:


(1 + m²)x² + (2mp)x + (p² - 1) = 0

Or cette équation ne doit pas avoir plus d'une solution, donc on impose au discriminant d'être nul, et on lie m et p par la relation suivante:

4m²p² - 4(1 + m²)(p² - 1) = 0


Ce qui peut se simplifier un peu:

p = +-;)(m² + 1)



On fait ensuite pareil pour l'autre cercle, en exprimant l'unicité de la solution en fonction de m et de p:
Un peu plus lourd:

(-10 + 2mp - 6m)² - 4(1 + m²)(24 - 6p + p²) = 0


En substituant p, on se ramène à une équation assez élaborée (j'ai pris p>0)


(-10 + 2m;)(m² + 1) - 6m)² - 4(1 + m²)(24 - 6;)(m² + 1) + (m² + 1)) = 0


On trouve deux solutions, et je pense que pour p< 0 on en trouve 2 autres.
T'as tes 4? tangentes... hum (j'ai pas trop regardé)


A vérifier...

Bonjour
Une autre démarche, sans doute pas mieux ...
On peut rechercher les droites d'équation y=ax+b ( ou ax-y+b=0) telles que la distance de O(0,0) à cette droite ainsi que la distance de A(5,3) à cette droite soient toutes les deux égales à 1
on utilise la formule qui donne la distance d'un point à une droite
on se retrouve avec à résoudre
b²=a²+1
(5a-3+b)²=a²+1
on a nécessairement (5a-3+b)²-b²=0
soit (5a-3)(5a-3+2b)=0
on a donc deux cas à envisager
d'abord avec a=3/5
b²=34/25
ce qui donne les équations des deux tangentes parallèles


ensuite pour le second cas
on a 5a-3+2b=0 et b²=a²+1
on est amené à résoudre une équation du second degré en a
on trouve a= ou a=
avec un peu de calcul, on trouve les équations des deux autres tangentes
sauf erreur on trouve
y = x -

y = x +

[bauzau]

Je n'ai pas vérifié vos calculs, mais ces méthodes sont loin d'être bidons!

Elles sont toutes les 2 bonnes, il reste juste à vérifier qu'aucune droite de la forme "x=a" est solution du pb:

pas besoin de conjecture:

Partons d'un point du 2iem cercle (qui n'est pas le cerlce trigo),

M(x,y) appartient au cercle

<=> (x-5)²+(y-3)²=1

=> (x-5)²<=1 ("plus petit ou égale")

=> -1<=x-5<=1

=> 4<=x<=6

On vient de prouver que si un point est sur le 2ieme cercle, alors son abscisse est plus grande que 4 (bien sur c'était facile à "voir" sur un graphique)

donc aucune droite d'équation "x=a" ne coupe les 2 cercles en même temps.


(rappel: tte droite du plan est de la forme y=ax+b ou bien x=a)

[LeJeu]

y = x -

y = x +

Racine de racine..... ca donne envie de simplifier
Surtout que ces tangentes passent par le milieu des deux cercles (5/2,3/2)

on remplace dans la première équation par exemple et on trouve
=

On vérifie en élevant au carré : c'est bien ok

et de même
=

[chan79]

Racine de racine..... ca donne envie de simplifier
Surtout que ces tangentes passent par le milieu des deux cercles (5/2,3/2)

on remplace dans la première équation par exemple et on trouve
=

On vérifie en élevant au carré : c'est bien ok

et de même
=

Bonjour
Bravo, c'est un peu plus simple :++:
Sinon, pour les coef de x, tu as une autre méthode ?

[Archytas]

Je vous remercie pour vos réponses, désolé de ne pas avoir répondu plus tôt, j'étais parti ! Je n'ai pas trop compris la méthode de chan79 :/. Pour ma part j'ai pensé à une soltution mais elle est assez imcomplète et plus laborieuse que les votres. Imcomplète parce que je n'ai que les tangentes parallèles :
On connait la distance aux deux centres :
On connait le rayon des cercles :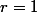
On applique Pythagore pour connaitre la dimension de l'hypothénuse "h" : du coup on sait que la tangente passe par les points solutions des systèmes :



Ce qui devrait nous donner 2 points et :



En ayant les deux autres points il suffit de résoudre un système de deux équations à deux inconnues pour avoir les équations.

Pour les deux autres je viens de comprendre que c'est possible avec pythagore encore mais cette fois nous avons l'hypthénuse (qui est la moitié de ce que j'ai appelé d) et on cherche un autre coté. Bref c'est long et chiant mais on atteint une réponse, mes neurones ne sont plus torturé =D

N'ayant pas tout compris de vos réponse j'espère ne pas vous avoir commis un plagiat de vos méthodes :S ! D'ailleurs si ce genre de problème vous amuse autant que moi j'avais fais un exercice du même type : "Trouver l'équation de la droite tangente au cercle trigonométrique (ou au cercle de centre (0;0) et de rayon 1) passant par le point d'absisse pi (pi;0)"

PS: Pourquoi n'est ce pas le cercle trigonométrique ? J'ai appris que c'était le cercle de centre (0;0) et de rayon 1 ni plus ni moins !
Bonne soirée et merci encore pour vos méthodes c'est toujours interessant d'avoir un maximum d'outil à sa portée pour abordr une nouvelle année parce que pythagore est bien utile mais il ne résoud pas tout le plus simplement !

[bauzau]

J
On applique Pythagore pour connaitre la dimension de l'hypothénuse "h" : du coup on sait que la tangente passe par les points solutions des systèmes :

euh... non? il me semble que par ces points-solutions passe une tangente à S1 qui passe par le centre du 2ieme cercle (et donc n'est pas tangent au 2ieme)


ps: oui ton premier cercle est bien S1

quante à la méthode de Lostounet: il s'agit de poser y=mx+p l'equation de la tangente commune,
cette tangente passe par un unique point du cercle, donc le systeme proposée possède une unique solution,
donc l'equation (1 + m²)x² + (2mp)x + (p² - 1) = 0 possède une unique solution (trinome du second degré: pour qu'il y ait une unique solution il faut que le discriminant soit nul)

on fait la meme chose avec l'autre cercle.
on obtient une équation

[bauzau]

Par contre ta méthode devrait fonctionner en divisant ton segment [CentreS1 CentreS2] en 2

voir image

http://img853.imageshack.us/img853/9529/tangentecommune.jpg

[chan79]

euh... non? il me semble que par ces points-solutions passe une tangente à S1 qui passe par le centre du 2ieme cercle (et donc n'est pas tangent au 2ieme)


ps: oui ton premier cercle est bien S1

quante à la méthode de Lostounet: il s'agit de poser y=mx+p l'equation de la tangente commune,
cette tangente passe par un unique point du cercle, donc le systeme proposée possède une unique solution,
donc l'equation (1 + m²)x² + (2mp)x + (p² - 1) = 0 possède une unique solution (trinome du second degré: pour qu'il y ait une unique solution il faut que le discriminant soit nul)

on fait la meme chose avec l'autre cercle.
on obtient une équation

Ce qui suit ne convient que si les deux cercles ont le même rayon. (ici, c'est 1)
D'abord un rappel
quand on a une droite d'équation ux+vy+w=0 et un point M(a,b)
la distance de M à la droite est donnée parla formule
distance =
PREMIER CAS
[img][IMG]http://img9.imageshack.us/img9/5985/azerty1.png[/img][/IMG]
ABCD et ABEF sont des rectangles. Les droites (AB), (CD) et (EF) sont parallèles.
Le coefficient drrecteur de (AB) est 3/5. Les deux tangentes ont le même coefficient directeur.
L'équation d'une tangente parallèle à (AB) est de la forme y=(3/5)x+m
soit 3x-5y+5m=0
La distance de ces tangentes à A(0,0) doit être 1 donc
=1
donc m= ou m=
Les équations sont
y =
y =
SECOND CAS
[img][IMG]http://img268.imageshack.us/img268/8591/37865213.png[/img][/IMG]
Soit I le milieu de [AB].On a: I(5/2;3/2)
I est centre de symétrie de la figure
Cherchons l'équation d'une droite de pente m qui passe par I.( la verticale qui passe par I ne convient pas)
y=mx+b
on remplace x et y par les coordonnées de I
3/2=m*5/2+b
b=3/2-5m/2
l'équation est
y=mx+3/2-5m/2
soit
2mx-2y+3-5m=0
La distance de A(0,0) à cette droite doit être égale à 1
on doit résoudre

(3-5m)²=4m²+4
9-30m+25m²=4m²+4
on arrive à cette équation du second degré
21m²-30m+5=0
= 225-5*21=120=4*30
m=
ou
m=
Il reste à remplacer m
première équation
y = x + -
SOIT y = x +
seconde équation
y = x + -
SOIT y = x -

[Archytas]

euh... non? il me semble que par ces points-solutions passe une tangente à S1 qui passe par le centre du 2ieme cercle (et donc n'est pas tangent au 2ieme)


ps: oui ton premier cercle est bien S1

quante à la méthode de Lostounet: il s'agit de poser y=mx+p l'equation de la tangente commune,
cette tangente passe par un unique point du cercle, donc le systeme proposée possède une unique solution,
donc l'equation (1 + m²)x² + (2mp)x + (p² - 1) = 0 possède une unique solution (trinome du second degré: pour qu'il y ait une unique solution il faut que le discriminant soit nul)

on fait la meme chose avec l'autre cercle.
on obtient une équation

Oui j'ai compris cette méthode c'est celle de chan79 que je n'avais pas compris avec l'histoire de la plus courte distance droite/point mais ça m'a été expliqué ! Je e comprends pas en quoi ma méthode ne fonctionne pas puisque on trouve une droite parallèle à la droite passant par le centre des deux cercles et elle les coupes chacun en un unique point.

Par contre ta méthode devrait fonctionner en divisant ton segment [CentreS1 CentreS2] en 2

voir image

http://img853.imageshack.us/img853/9529/tangentecommune.jpg

Oui, c'est la méthode dont je parlais pour quand les deux tangentes se croisaient. Et elle marche tout de même pour les tangentes parallèles !

[bauzau]

On connait la distance aux deux centres :
On connait le rayon des cercles :
On applique Pythagore pour connaitre la dimension de l'hypothénuse "h" : du coup on sait que la tangente passe par les points solutions des systèmes :

Effectivement c'est moi qui t'avait mal compris, ca marche

[chan79]

Bonne soirée et merci encore pour vos méthodes c'est toujours interessant d'avoir un maximum d'outil à sa portée pour abordr une nouvelle année parce que pythagore est bien utile mais il ne résoud pas tout le plus simplement !

Bonjour
Un petit complément pour les tangentes qui se croisent.
[img][IMG]http://img43.imageshack.us/img43/1999/37966715.png[/img][/IMG]
Si on appelle C le milieu de [AB] on trace le cercle rouge de diamètre [AC]
Il coupe le cercle de centre A et de rayon 1 en E et F.
Puisque AEC et AFC sont rectangles en E et F, les droites (FC) et (EC) sont bien les tangentes cherchées.
On peut donc déterminer les coordonnées de E et F en considérant que ce sont les points d'intersection du cercle rouge et du cercle trigonométrique.
Tu tomberas sur le sytème
x²+y²=1
(x-5/4)²+(y-3/4)²=34/16

[Dlzlogic]

Bonjour,
Petite intervention personnelle.
Il y a une spécialité qui utilise beaucoup ce type de calcul en géométrie cartésienne, c'est celle des géomètres. Il se trouve que on n'utilise jamais les équations de droite, de cercle, de parabole.
Les méthodes utilisées sont celle détaillées par chan79 : on trouve un ou des points qui répondent à la question, en l'occurrence l'intersection de 2 cercles, on calcule leurs coordonnées, on fait la même chose pour l'autre cercle, on obtient ainsi 4 points (si les 2 cercles sont strictement extérieurs). Ces 4 points définissent 4 segments, si on veut on peut calculer les équations des droites supports de ces 4 segments.
Dans les applications informatiques de calcul de ce type, personnellement, je n'ai jamais utilisé les équations de droite, cercle etc. Si on veut définir une droite, on peut la définir par "passant par 2 points" ou "passant par un point et de direction donnée".
Cependant il est aussi absolument indispensable de connaitre parfaitement ces méthodes basées sur les équations de droite, cercle, parabole, ellipse, clotoïdes etc.

[Archytas]

Cependant il est aussi absolument indispensable de connaitre parfaitement ces méthodes basées sur les équations de droite, cercle, parabole, ellipse, clotoïdes etc.

Je n'en suis pas à ce niveau là !

[Dlzlogic]

Je n'en suis pas à ce niveau là !

Oh, mais aucun problème, je tenais juste à évoquer différentes fonctions pour essayer de montrer que c'est vrai dans tous les cas.
Mais il ne faut surtout pas oublier que l'étude par les fonction est un point de passage obligé si on veut avoir une vue générale de l'ensemble.

[chan79]

Un autre exo du même genre à conseiller mais pour plus tard, car là, c'est la rentrée:
Déterminer les équations des tangentes conmmunes à ces deux cercles:
le cercle de centre (3,1) et de rayon 2
le cercle de centre (8,2) et de rayon 3
cadeau (une fois le fichier chargé, animer en cliquant sur le bouton en bas à gauche)

[valu24]

exo 44 . détermination des coordonnées du point d'intersection de deux droites.
Le plan est rapporté à un repère et les droites D et D' sont sécantes et non parallèles à l'axe des ordonnées , sont données par leurs équations réduites.

1. D : y = 2x + 2 et D' : y = 5x - 2

a) Ecrire l'égalité entre les deux seconds membres de ces équations puis calculer l'abscisse x du point d'intersections

b) reporter sa valeur dans l'une des deux équations réduites pour calculer l'ordonnée y de ce point

c) en déduire les coordonnées du point d'intersection des deux droites

2. Suivre la démarche précédente pour

a) D : y = 2x + 1 ; D' : y = - 3x - 9
b) D : y = 4x - 1 ; D' : y = x + 3,2