Systèmes linéaires

[Seb111279]

Bonjour,

Je suis en train de préparer un concours dans la fonction publique.
Pour cela, il est nécessaire de réviser les systèmes linéaires de 2 équations à 2 inconnues et de 3 équations à 3 inconnues. Il est précisé qu'on ne peut pas utiliser le pivot de gauss pour les résoudre. Je voulais savoir si la méthode de substitution et la résolution par le pivot de gauss sont deux méthodes identiques ? Si oui par quelle autre méthode peut-on résoudre ces systèmes linéaires.

Merci par avance.

[Dinozzo13]

Salut !
Non, ce sont des méthodes différentes.
Pour ma part, j'utilise toujours la méthode des déterminants qui est infaillible, sauf en cas d'erreurs de calculs.

Soit S le système suivant :

Tu calcules le détermiannt D du système :
Esuite, on a deux choix :
1°) Si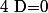 alors il y a soit une infinité de solutions, soit aucune.
Si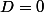 alors il existe un réel k tel que et .
Il faut donc calculer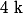 pour savoir si .
Si c'est le cas, alors il y a une infinité de solutions.
Sinon, il n'y en a aucune.
2°) Si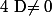 alors il existe un unique couple solution de (S).
Tu calcules deux autres déterminants :



Ainsi, le couple solution est :
et

Voilà, :++:

[busard_des_roseaux]

Bonjour,

comme méthodes, il y a
- combinaisons linéaires dont pivot De Gauss
- déterminants (règle de Sarrus)
- substitution

et quelques "astuces" quand le système est symétrique
comme de faire apparaitre la valeur de la somme des inconnues
comme égalité supplémentaire

[Arnaud-29-31]

Bonjour,

La méthode du pivot de Gauss décrit une façon spéciale de s'organiser et d'utiliser la méthode par combinaison ... Ceci revient à trianguler le système.

Cela m'étonnerait beaucoup que cette méthode soit proscrite dans le but d'orienter le candidat vers une résolution par substitution ...

A quel niveau est ce concours ?

[Seb111279]

Merci beaucoup à vous tous pour ces réponses. Cela me parait déjà plus clair.
Pour Arnaud : le concours que je prépare est celui de technicien supérieur territorial. Voici un copié-collé du programme pour la partie algèbre :

2 : Algèbre
2.1. Opérations sur les polynômes : développement et factorisation.
2.2. Identités remarquables du second degré.
2.3. Equations et inéquations du premier et du second degré à une inconnue.
2.4. Systèmes linéaires de 2 équations à 2 inconnues, 3 équations à 3 inconnues (sans utilisation du pivot de Gauss).

Encore merci à vous.

[busard_des_roseaux]

2.4. Systèmes linéaires de 2 équations à 2 inconnues, 3 équations à 3 inconnues (sans utilisation du pivot de Gauss).

Salut !

tu as mal interprété le libellé du programme. ça veut dire que le pivot
de Gauss n'est pas au programme et ne sera pas enseigné.
Mais il n'est pas interdit de l'utiliser puisque
la technique du pivot est un cas particulier d'une méthode générale
de résolution de systèmes qui s'appelle "combinaison linéaire d'équations"

[Seb111279]

Salut !

tu as mal interprété le libellé du programme. ça veut dire que le pivot
de Gauss n'est pas au programme et ne sera pas enseigné.
Mais il n'est pas interdit de l'utiliser puisque
la technique du pivot est un cas particulier d'une méthode générale
de résolution de systèmes qui s'appelle "combinaison linéaire d'équations"

Je l'avais pas interprété de cette façon. Tu dois sans doute avoir raison. En tout cas me voilà rassuré. Merci. :++: