[TS] Systemes lineaires
15 messages
- Page 1 sur 1
[TS] Systemes lineaires
Hello everybody
Je sais qu'un systeme lineaire peut avoir une solution, aucune solution ou une infinité de solution. Parmi les infinités de solution, il y'a des infinités de type "droite" et de type "plan".
- Comment faire la différence "analytiquement" entre une infinité de type "droite" et une de type "plan"? Selon le nbre de parametres dans l'ensemble des listes solutions?
- N'existe-t-il pas d'autres types d'"infinités"? Ex: Ne dirait-on pas d'un système dont l'ensemble des triplets solutions est R^3 qu'il s'agit d'une infinité de type "espace"? (au passage, pouvz-vs me donner un exemple de systeme dont l'nsemble des solutions est R^3?)
- Peut-on parler d'infinité de type droite ou plan lorque le système est à plus de 3 inconnues? On est plus dans les 3 dimensions...
MERCI
Je sais qu'un systeme lineaire peut avoir une solution, aucune solution ou une infinité de solution. Parmi les infinités de solution, il y'a des infinités de type "droite" et de type "plan".
- Comment faire la différence "analytiquement" entre une infinité de type "droite" et une de type "plan"? Selon le nbre de parametres dans l'ensemble des listes solutions?
- N'existe-t-il pas d'autres types d'"infinités"? Ex: Ne dirait-on pas d'un système dont l'ensemble des triplets solutions est R^3 qu'il s'agit d'une infinité de type "espace"? (au passage, pouvz-vs me donner un exemple de systeme dont l'nsemble des solutions est R^3?)
- Peut-on parler d'infinité de type droite ou plan lorque le système est à plus de 3 inconnues? On est plus dans les 3 dimensions...
MERCI
Bonjour 
Rappellons que résoudre le systéme affine :
\{{a_{11}x_{1}+...+a_{1p}x_{p}=b_{1}\\ ... \\ ... \\a_{n1}x_{1}+...+a_{np}x_{p}=b_{n})
d'inconnues\in K^{p})
revient à résoudre l'équation matricielle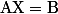 avec :
avec :
, B=\begin{pmatrix}b_{1}\\.\\.\\.\\b_{n}\end{pmatrix}\in M_{n,1}(K) et X=\begin{pmatrix}x_{1}\\.\\.\\.\\x_{n}\end{pmatrix}\in M_{p,1}(K))
Le Système est dit de Cramer si n=p=rg(A). La matrice A est carrée et inversible est le systéme admet alors une unique solution.
dans le cas où rg(A)=n<p, A est inversible et l'ensemble S des solutions de (S) est un sous-espace affine de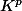 de dimension p-r
de dimension p-r
dans le cas où rg(A)<n, on peut procéder par combinaisons linéaires pour se ramener au cas précédent.
Dans le cas où les seconds membres sont nuls le systéme admet une solution triviale (0,....,0) et l'ensemble des solutions est un sev de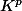 de dimension p-rg(A) . En particulier le sy stéme admet une solution autre que celle-ci si et seulement si rg(A)<p .
de dimension p-rg(A) . En particulier le sy stéme admet une solution autre que celle-ci si et seulement si rg(A)<p .
Un plan est un hyperplan de (un sous espace affine de dimension
(un sous espace affine de dimension -1=2) ) . Une droite est un hyperplan de
) . Une droite est un hyperplan de  (donc un sea de dimension
(donc un sea de dimension -1=1) )
)
Un systéme dans l'ensemble des solutions est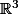 :
:
Tout simplement :
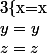

Comme je l'ai dit, ton ensemble de solution peut trés bien être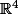 ou un sea de
ou un sea de 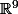 . Mais aprés ils n'ont plus de représentation géométrique.
. Mais aprés ils n'ont plus de représentation géométrique.
Oui, par exemple le systéme :
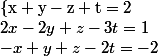 d'inconnues x,y et z dans
d'inconnues x,y et z dans 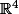 et de paramétre réel t admet pour solution :
et de paramétre réel t admet pour solution :
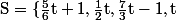,t\in\mathbb{R}\}) qui est la droite affine de
qui est la droite affine de 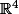 passant par le point (1,0,-1,0) et dirigée par le vecteur (5,3,14,6) par exemple.
passant par le point (1,0,-1,0) et dirigée par le vecteur (5,3,14,6) par exemple.

Jord
Rappellons que résoudre le systéme affine :
d'inconnues
revient à résoudre l'équation matricielle
Le Système est dit de Cramer si n=p=rg(A). La matrice A est carrée et inversible est le systéme admet alors une unique solution.
dans le cas où rg(A)=n<p, A est inversible et l'ensemble S des solutions de (S) est un sous-espace affine de
dans le cas où rg(A)<n, on peut procéder par combinaisons linéaires pour se ramener au cas précédent.
Dans le cas où les seconds membres sont nuls le systéme admet une solution triviale (0,....,0) et l'ensemble des solutions est un sev de
- Comment faire la différence "analytiquement" entre une infinité de type "droite" et une de type "plan"? Selon le nbre de parametres dans l'ensemble des listes solutions?
Un plan est un hyperplan de
- N'existe-t-il pas d'autres types d'"infinités"? Ex: Ne dirait-on pas d'un système dont l'ensemble des triplets solutions est R^3 qu'il s'agit d'une infinité de type "espace"? (au passage, pouvz-vs me donner un exemple de systeme dont l'nsemble des solutions est R^3?)
Un systéme dans l'ensemble des solutions est
Tout simplement :
Comme je l'ai dit, ton ensemble de solution peut trés bien être
- Peut-on parler d'infinité de type droite ou plan lorque le système est à plus de 3 inconnues? On est plus dans les 3 dimensions...
Oui, par exemple le systéme :
Jord
Je ne suis pas loin d'avoir peur quand je lis les explications de Nightmare ... je comprends à peu près ce qu'il raconte pour avoir lu des vieux bouquins du temps où la TS était difficile, mais quand même .... t'es sûr que t'es qu'en 1ère S (ou TS) ?
Les matrices ne sont théoriquement même plus au programme en série S ...
Je vais devenir parano si tous les matheux deviennent comme ça :D vite, je plonge dans mes livres de MPSI !
Les matrices ne sont théoriquement même plus au programme en série S ...
Je vais devenir parano si tous les matheux deviennent comme ça :D vite, je plonge dans mes livres de MPSI !
Je suis partage (i am partaged...) entre l'admiration et (mais ca c'est quand ma mauvaise foi reprend le dessus) la colere...
Et oui lors de la remise des cerveaux a la naissance je devais etre en train de dormir , paske moi en seconde a part arriver a calculer des pourcentages (et encore...) ben j'etais nul (i was useless).
chapo
Et oui lors de la remise des cerveaux a la naissance je devais etre en train de dormir , paske moi en seconde a part arriver a calculer des pourcentages (et encore...) ben j'etais nul (i was useless).
chapo
lol! je suis en prépa, et d'habitude les félicitations de ce genre me sont adressées lol(bien que je ne sois pas vraiment un passioné des maths)...mais la je suis totalement sur le cul....aa tel point que je ne suis franchement pas convaincu que tu sois vraiment en 1ere S...
Tu dois t'ennuyer a mourrir en cours (sauf si tu n'y vas presque pas comme c'était mon cas! ;) )
Enfin je crois que quelqu'un comme toi a sa place dans une prépa ou on pousse les élèves! Et franchement, tu a toutes les chances de décrocher les toutes meilleurs écoles ! :++: lol
Pour l'instant je ne regrette pas de m'etre consacré a apprendre le plus de choses possible dans tous les domaines...quand l'heure du concours viendra j'espere que ca ne changera pas!lol
Pas la peine de te souhaiter bonne chance pour la suite...pas besoin du tout :ptdr:
Tu dois t'ennuyer a mourrir en cours (sauf si tu n'y vas presque pas comme c'était mon cas! ;) )
Enfin je crois que quelqu'un comme toi a sa place dans une prépa ou on pousse les élèves! Et franchement, tu a toutes les chances de décrocher les toutes meilleurs écoles ! :++: lol
Pour l'instant je ne regrette pas de m'etre consacré a apprendre le plus de choses possible dans tous les domaines...quand l'heure du concours viendra j'espere que ca ne changera pas!lol
Pas la peine de te souhaiter bonne chance pour la suite...pas besoin du tout :ptdr:
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
