Système d'équation

[Anonyme]

Bonsoir,
Dans le système suivant, comment poursuivre?
Merci d'avance!

[Anonyme]

Bonsoir,
Dans le système suivant, comment poursuivre?
Merci d'avance!

a) Avec la ligne 2) tu trouves x en fonction de y.

b) Avec les ligne 1) et 3) que tu soustrait ou additionne, tu elimines y² ou x² : ca te donne 2 solutions de x ou y.

c)Ensuite pour trouver le deuxieme inconnu tu utilises le a) en remplacant x ou y par ce que tu viens de trouver en b).

Au final tu as 2 solutions pour x et 2 solutions pour y.

[Anonyme]

Bon ... en réalité, j'ai quelques petits soucis...

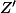
Afin de trouver les racines carrées des complexes et , j'ai procédé comme cela:

Soit 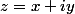la racine de cherchée.





Je trouve à la fin:




Cela me paraît assez...compliqué... Qu'en pensez-vous? Et en plus, je l'ai fait pour et pas encore pour ...

[Anonyme]

Tes resulats me semblent justes mais je ne vois pas pourquoi tu vas chercher des complexes...j'imagine qu'il s'agit d'une autre partie de ton exercice...

[Anonyme]

Bon, en réalité, voici l'énoncé de mon exercice:


1°) Résoudre l'équation .
2°) Ecrire comme le produit de 2 polynômes à coefficients réels.


De ce fait....je cherche à trouver les solutions de l'équation, et j'ai posé


Et je cherchais donc à obtenir les racines carrées afin d'avoir les solutions de l'équation posée...mais voilà...je n'y parviens point... comment faire?

[Anonyme]

Recapitulons:

Question 1)

Tu pose Z=z², ca te donne l'equation 3Z² + 2Z +1= 0 à resoudre:

Son delta = 2²-4*3= -8=8i²
Donc les 2 solutions sont: Z= (-1 + i*sqrt(2))/3 et Z'= (-1 -i*sqrt(2))/3

Puis comme Z=z² tu trouves 2 solutions pour z : z= +/- sqrt(Z)
Idem pour Z'=z'² tu trouves: z' = +/- sqrt(Z')

Tu as donc trouves les 4 solutions de cette equations.


Question 2)

Maintenant que tu as ces 4 solutions, tu peux factoriser ton polynome avec leur aide: 3z^4 + 2z² +1= 0 <==> (z-z1)*(z-z2)*(z-z3)*(z-z4)=0 avec z1,z2,z3,z4 tes 4 solutions trouvees plus haut.

Maintenant tu developpes un peu pour eliminer les termes en i (i²=-1) et obtenir les 2 polynomes à coeficients uniquement reels demandes.

[phenomene]

Bonsoir,
Dans le système suivant, comment poursuivre?
Merci d'avance!

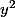
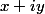
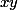
Oui, c'est la bonne méthode pour obtenir les racines carrées d'un nombre complexe. En additionnant et en soustrayant les première et troisième équations, tu détermines et . Tu peux en déduire a priori quatre valeurs possibles pour , puisqu'on obtient et à un signe près. Mais la deuxième équation impose une condition sur le signe de (ici ils doivent être de même signe), si bien qu'on n'a en vérité que deux solutions. Cela tombe bien, puisqu'un complexe non nul a exactement deux racines carrées. :++: