est ce que quelqu'un pourrais me dire comment montrer que deux fonctions sont symetriques par rapport à une autre fonction ???
merci d'avance
Symetrie de deux fonction
11 messages
- Page 1 sur 1
il ya une methode purement algebrique, sinon si tu as une fonction et sa reciproque ( exemple x² et x^0,5 ) alors elles sont symetriques a la droite dequation Y=x
en effet tu a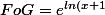} - 1 = x+1-1= x)
tu as donc les deux fonctions sont reciproques donc symetrique a Y=x pour tout x appartenant a lintersection de leurs ensembles de definition
les deux fonctions sont reciproques donc symetrique a Y=x pour tout x appartenant a lintersection de leurs ensembles de definition
en effet tu a
tu as donc
comment ça ???? je sais qu'ellls sont symetriques c sur mais faut que je le montre mais je ne sais pas le montrer
d'apres mon cours je sais que ln(x) et e^x sont symetrique par rapport a y=x mais j'ai pas de formule apres pour appliquer la symetrie apres ..........
autre chose est cce que vous pouvez me dire si la primitive de -e^(x)=-e^(x)???
d'apres mon cours je sais que ln(x) et e^x sont symetrique par rapport a y=x mais j'ai pas de formule apres pour appliquer la symetrie apres ..........
autre chose est cce que vous pouvez me dire si la primitive de -e^(x)=-e^(x)???
une primitive de e^x est e^x +k où k est un réel quelconque
"tu sais" qu'elles sont symétriques, et "on te demande de le démontrer" ... donc tu ne le sais pas; alors fais comme je te dis, parce que des courbes sont symétriques par rapport à la droite y=x lorsque l'échange des coordonnées de tout point de l'une donne un point de l'autre
"tu sais" qu'elles sont symétriques, et "on te demande de le démontrer" ... donc tu ne le sais pas; alors fais comme je te dis, parce que des courbes sont symétriques par rapport à la droite y=x lorsque l'échange des coordonnées de tout point de l'une donne un point de l'autre
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
