Bonjour,
J'ai un DM de maths à faire. Dans un exercice je dois faire un tableau de variation donc je dérive e^x+1/x ça donne e^x-1/x^2 puis je trouve leur signe.
e^x est strictement positif mais je ne trouve pas le signe de-1/x^2 donc je bloque pour la suite pouvez vous m'aider svp
Merci
Dm sur les exponentielles
8 messages
- Page 1 sur 1
Re: Dm sur les exponentielles
salut,
=e^x +\dfrac{1}{x})
=\dfrac{x^2 e^x-1}{x^2})
on pose=x^2 \, e^{x})
La dérivée h' vaut:=e^x \, x (x+2))
On étudie le signe de la dérivée h' puis les variations de h.
Le tableau de variation de h indique qu'il existe un unique tel que
tel que =1)
Des variations de h , on en déduit le signe de f' (on résout l'inéquation \geq 1) ):
):
La dérivée f' est négative sur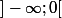 , non définie en 0, négative sur
, non définie en 0, négative sur  et positive sur
et positive sur 
on pose
La dérivée h' vaut:
On étudie le signe de la dérivée h' puis les variations de h.
Le tableau de variation de h indique qu'il existe un unique
Des variations de h , on en déduit le signe de f' (on résout l'inéquation
La dérivée f' est négative sur
Modifié en dernier par mathelot le 25 Mai 2020, 19:52, modifié 7 fois.
Re: Dm sur les exponentielles
Bonjour,
il n'est pas utile d'ouvrir un nouveau post à chaque fois que l'on te réponds car il est alors difficile de suivre le sujet .
lycee/sur-les-exponentielles-t218407.html
il n'est pas utile d'ouvrir un nouveau post à chaque fois que l'on te réponds car il est alors difficile de suivre le sujet .
lycee/sur-les-exponentielles-t218407.html
Re: Dm sur les exponentielles
Modifié en dernier par mathelot le 25 Mai 2020, 19:49, modifié 2 fois.
Re: Dm sur les exponentielles
f(x) = e^x + 1/x
f'(x) = e^x - 1/x²
f'(x) = (x²*e^x - 1)/x² = (x* e^(x/2) - 1).(x* e^(x/2) + 1)/x²
1°) pour x < 0,
g(x) = x* e^(x/2) + 1
g'(x) = e^(x/2)*(x/2 + 1) --> g est min en x = -2, ce min est g(-2) = 1 - 2/e > 0 et donc (e^(x/2)*(x/2 + 1)) > 0
et comme (x* e^(x/2) - 1)/x² < 0, f'(x) < 0 --> f est décroissante. (sur ]-oo ; 0[)
2°) pour x > 0
f''(x) = e^x + 2/x³
f''(x) > 0 et donc f' est croissante
f'(x) = 0 pour x* e^(x/2) = 1 (donc pour x = alpha (presque égal 0,7035)) -->
f'(x) < 0 pour x dans ]0 ; alpha[ --> f est décroissante
f'(x) = 0 pour x =a alpha
f'(x) > 0 pour x > alpha -> f est croissante

f'(x) = e^x - 1/x²
f'(x) = (x²*e^x - 1)/x² = (x* e^(x/2) - 1).(x* e^(x/2) + 1)/x²
1°) pour x < 0,
g(x) = x* e^(x/2) + 1
g'(x) = e^(x/2)*(x/2 + 1) --> g est min en x = -2, ce min est g(-2) = 1 - 2/e > 0 et donc (e^(x/2)*(x/2 + 1)) > 0
et comme (x* e^(x/2) - 1)/x² < 0, f'(x) < 0 --> f est décroissante. (sur ]-oo ; 0[)
2°) pour x > 0
f''(x) = e^x + 2/x³
f''(x) > 0 et donc f' est croissante
f'(x) = 0 pour x* e^(x/2) = 1 (donc pour x = alpha (presque égal 0,7035)) -->
f'(x) < 0 pour x dans ]0 ; alpha[ --> f est décroissante
f'(x) = 0 pour x =a alpha
f'(x) > 0 pour x > alpha -> f est croissante
Re: Dm sur les exponentielles
.
Modifié en dernier par mathelot le 25 Mai 2020, 20:28, modifié 1 fois.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

