SUites du type U(n+1)=aUn+b

[Arconada]

Bon je vous expliques mon problème mon profeeseur c'est dit que se serais bien de nous donner un DM sur les suites sans que l'on est est encore étudié donc je comprend la toute première question mais pas plus donc si vous pourriez m'aider car je suis complètement largué la,merci d'avance pour tout:

A)Soit (Un)n>(ou égal)0 la suite définie par Uo(réel donné) et
U(n+1)=f(Un) avec f(x)=ax+ , a réel donné non nul, b rél donné quelconque.
1)Quelle est la nature de (Un) dans le cas ou a=1 et dans le cas ou b=0?
2)Montrer que dans l'équation f(x)=x possède,en général,une solution unique A.
DOnneer une interprétation géométrique de A et des cas d'exception.
Si U0=A,que peut on dire de la suite (Un)?
3)On suppose que A existe et que U0 différent de A et l'on pose :Vn=Un-A,pour tout n appartenant N.
Montrer que la suite (Vn) est géométrique.
Montrer que (Un) est convergente ssi (Vn) est convergente.
A quelles conditions sur a et b , (Vn) est elle convergente et quelles sont alors les limites de (Vn) et de (Un)?

Merci de vôtre compréhension et de vôtre aide,
Arconada!

[becirj]

Quelques indications

2.Tu as simplement à résoudre l'équation ax+b=x.
2 cas à envisager a=1 et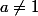
Graphiquement cela revient à étudier l'intersection des droites d'équations y=ax+b et y=x

Si ,regarde les termes suivants puis une toute petite récurrence !

3. Il faut exprimer en fonction de
On part de
Comme il faut exprimer en fonction de on utilise la relation donnée en "l'inversant" : 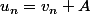et en remplaçant A par son expression tu arriveras à la solution.

Une suite converge si elle a une limite finie l donc l'équivalence est immédiate.

Une suite géométrique converge ssi sa raison appartient à l'intervalle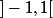 et sa limite est alors nulle