Suites arithmétiques

[poincaré]

Bonjour tout le monde.

Comme vous devez vous en douter j'ai un petit problème à résoudre.

Consigne : Déterminer trois entiers relatifs consécutifs dont la somme égale le produit.

Pour ma part j'ai posé le problème tel quel :

Soit x un entier.
Les trois entiers sont donc :
x
x+1
x+2

On veut donc :
(x)+(x+1)+(x+2)=(x)*(x+1)*(x+2).

a ce stade la je suis bloqué. Dois-je dévelloper ? si c'est le cas cela ne me mene a rien (du moins je n'y voit pas la nécéssitée).

Merci d'avance.

salutations.

[BancH]

Fais pareil avec

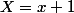
[flaja]

l'équation se simplifie et donne une équation du 2ème degré

[poincaré]

si on dévellope cela fait :

3x+3 = x^3 + 3x^2 + 2x.

C'est un polynôme du troisieme degrès je n'arrive pas a le mettre au second degrès.

[BancH]

[BancH]

Résouds maintenant !

[BancH]

si on dévellope cela fait :

3x+3 = x^3 + 3x^2 + 2x.

C'est un polynôme du troisieme degrès je n'arrive pas a le mettre au second degrès.

[poincaré]

C'est le résultat que je trouve aussi.
Excusez moi, mais je suis long a la détente, comment résoudre cela ?
si mon petit cerveau comprend bien, il faut élever au cube X - X et cela donne 3X ?
Merci pour le temps que vous m'accordez.

[BancH]

Comment résouds-tu: ?

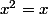
[poincaré]

si x^2 = x
alors x = 0 ou x = 1
equivaut
x^2 - x = 0

[BancH]

Non attends, on va faire autre chose:


Factorise

[poincaré]

la factorisation : x(x^2+1-3)
soit x(x^2 - 2)

[BancH]

Maintenant simplifie de la même façon

[poincaré]

3x = x^3 - x
x^3 - 4x = 0
x(x^2 - 4) = 0
ce produit est nul si un des deux thermes est nul.
x^2 = 4
donc x = 2 ou x = -2 ?

[BancH]

Ouais c'est ça.





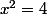
Il fallait diviser par !

[poincaré]

Merci de votre patience Monsieur (Madame) je vous en suis très reconnaissant.

:happy2:

salutations, et encore merci !