[Défi Lycée] Suite super croissante
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Aoû 2009, 10:58
par Clembou » 16 Aoû 2009, 10:58
Bonjour à tous,
J'ai vu que Busard donnait des défis aux collégiens et lycéens. Voici mon défi assez facile.
On dit qu'une suite
_{n \in \mathbb{N}})
est super croissante si
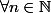
,
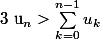
Montrer que
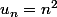
est super croissante.
d'après :
Ainsi de Suite de Stéphane Pasquet
Exercice érroné, voir les messages 3 et 4
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 16 Aoû 2009, 11:16
par Timothé Lefebvre » 16 Aoû 2009, 11:16
Salut les gars !
A ce que je vois c'est parti pour une serie de defis, attendez une petite semaine que je rentre enfin a la civilisation, j'en ai pleins de sympas chez moi !
 par busard_des_roseaux » 16 Aoû 2009, 11:33
par busard_des_roseaux » 16 Aoû 2009, 11:33
Bonjour Clément !
es-tu certain ? le sigma est asymptotiquement en
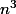
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Aoû 2009, 11:36
par Clembou » 16 Aoû 2009, 11:36
busard_des_roseaux a écrit:Bonjour Clément !
es-tu certain ? le sigma est asymptotiquement en
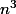
Voilà ! C'est ce que je me suis dit en résolvant cet exo... C'est dans le bouquin "Ainsi de suite" de Stéphane Pasquet (
http://mathweb.fr). Ca ne marche pas pour
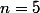
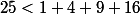
Bref, l'exercice est érroné. Merci Busard pour cette remarque :++:
 par busard_des_roseaux » 16 Aoû 2009, 11:55
par busard_des_roseaux » 16 Aoû 2009, 11:55
bon,
nouvel exo :we: :
trouver un exemple de suite super-croissante.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Aoû 2009, 12:09
par Clembou » 16 Aoû 2009, 12:09
Des suites téléscopiques ?
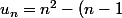^2)
...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 16 Aoû 2009, 12:10
par Ericovitchi » 16 Aoû 2009, 12:10
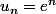
marche
-
Switch87
- Membre Relatif
- Messages: 229
- Enregistré le: 24 Nov 2008, 00:15
-
 par Switch87 » 16 Aoû 2009, 18:14
par Switch87 » 16 Aoû 2009, 18:14
Ericovitchi a écrit: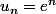
marche
Ben si on veut partir comme des fous, factorielle n marche aussi...
Sinon, un exemple en dessous de e^n, il y a 2^n, et ce doit être le plus petit a tel que a^n soit super croissante.
Quelqu'un trouve encore plus petit?
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 16 Aoû 2009, 18:30
par Jack the ripper » 16 Aoû 2009, 18:30
En quoi consistent ces défis? Je veux dire, est-ce que ce sont des exercices typiques du lycée ou se rapprochant plus d'exercices de logique ou d'Olympiades par exemple? - qui m'ont bien embêté au passage -.
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 16 Aoû 2009, 19:13
par Clembou » 16 Aoû 2009, 19:13
Jack the ripper a écrit:En quoi consistent ces défis? Je veux dire, est-ce que ce sont des exercices typiques du lycée ou se rapprochant plus d'exercices de logique ou d'Olympiades par exemple? - qui m'ont bien embêté au passage -.
Défi parce que c'est pas un exercice qu'on retrouve typiquement dans les programems officiels... Mais ce n'est pas d'une difficulté aussi elevée que l'olympiades :triste:
-
Jack the ripper
- Membre Relatif
- Messages: 211
- Enregistré le: 11 Mai 2008, 12:02
-
 par Jack the ripper » 16 Aoû 2009, 19:16
par Jack the ripper » 16 Aoû 2009, 19:16
D'accord. C'est sûr que les Olympiades c'est autre chose... Beaucoup quittaient la salle au bout de 2 heures.
-
xyz1975
- Membre Rationnel
- Messages: 555
- Enregistré le: 15 Sep 2007, 21:30
-
 par xyz1975 » 16 Aoû 2009, 20:24
par xyz1975 » 16 Aoû 2009, 20:24
Un simple exemple :
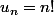
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 16 Aoû 2009, 20:34
par Matt_01 » 16 Aoû 2009, 20:34
Si je ne m'abuse, "la plus petite" suite supercroissante avec
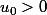
est
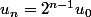
pour
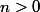
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 16 Aoû 2009, 21:14
par skilveg » 16 Aoû 2009, 21:14
J'ai aussi l'impression que c'est le cas: on doit avoir
)
, où
)
est une suite strictement positive. Donc en réécrivant les sommes
\geq 2^{n-1}a_0)
, d'où le résultat.
-
Switch87
- Membre Relatif
- Messages: 229
- Enregistré le: 24 Nov 2008, 00:15
-
 par Switch87 » 16 Aoû 2009, 22:28
par Switch87 » 16 Aoû 2009, 22:28
Ouais, je donnais 2^n en démarrant à U1, c'est kif-kif.
 par busard_des_roseaux » 17 Aoû 2009, 08:04
par busard_des_roseaux » 17 Aoû 2009, 08:04
re,
au pif, j'ai envie de dire qu'il n'existe pas de "plus petite suite", parce que
l'inégalité est stricte et que l'ensemble de ces suites est un ouvert (???)
:doh:
ps: on peut toujours définir la distance de deux suites comme
=\sum_{n=0}^{\infty} \, 2^{-n} \, \frac{|u_n-v_n|}{1+|u_n-v_n|})
car
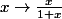
prend ses valeurs dans [0;1[
sur
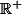
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 17 Aoû 2009, 08:11
par skilveg » 17 Aoû 2009, 08:11
On parlait de plus petite suite au sens asymptotique du terme. Sinon, j'ai surtout l'impression que l'ensemble de ces suites est une intersection dénombrable d'ouverts, qui a donc très peu de chances d'être ouverte (en tout cas pour la topo produit).
 par busard_des_roseaux » 17 Aoû 2009, 08:20
par busard_des_roseaux » 17 Aoû 2009, 08:20
skilveg a écrit:l'ensemble de ces suites est une intersection dénombrable d'ouverts
oui, je n'avais pas vû l'intersection :hum: mais elle est non vide...
au fait
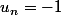
:zen:
-
Switch87
- Membre Relatif
- Messages: 229
- Enregistré le: 24 Nov 2008, 00:15
-
 par Switch87 » 17 Aoû 2009, 12:43
par Switch87 » 17 Aoû 2009, 12:43
lol, bien vu si on commence la somme à k=1
sinon, on a un problème pour u1.
;)
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 17 Aoû 2009, 12:46
par skilveg » 17 Aoû 2009, 12:46
Non, nécessairement
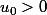
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
est super croissante si
,
est super croissante.
