Suite de Fibonacci

par **cocmarseillais** » 19 Mai 2009, 15:16

Bonjour a tous,

je rencontre de gros problèmes pour résoudre un dm sur la suite de fibonacci, c'est pourquoi je viens solliciter votre aide. Voici la question a laquelle je bloque:

a) démontrer que pour tout n et u1= 1 et u2= 2, on a: u(n+2) = u(n+1) + u(n)
{les expressions entre parenthèses sont normalement en indice}

merci beaucoup et bonne fin de journée

par **maturin** » 19 Mai 2009, 15:42

euh il manque qqch dans ton énoncé.

Il faudrait que tu nous donnes ta définition de u(n).

par **Zweig** » 19 Mai 2009, 15:46

Salut,

C'est pourtant la définition même de la suite de Fibonacci ... mais peut-être qu'on t'a donné la valeur de

, c'est-à-dire :

Dans ce cas, pose

et

. On a donc

. Exprime

et

en fonction de

et

. Tu en déduis alors la relation demandée.

par **cocmarseillais** » 19 Mai 2009, 15:52

Tout d'abord merci d'avoir répondu.

Le sujet c'est une puce qui se déplace sur des cases de 0 à n (d'une ou deux cases a la fois sans reculer) et on voudrait connaitre le nombre de de chemins possibles qui conduisent a la case n. Ensuite on me demande donc de démontrer que u(n+2) = u(n+1) +u(n) compte tenu que u(1)=1 et u(2)=2.

par **maturin** » 19 Mai 2009, 16:04

c'est pas clair.
c'est quoi la suite u dans ce cas si n représente les cases ?

par **maturin** » 19 Mai 2009, 16:08

Ben pour arriver sur la dernière case n+2 elle fait soit un bond de 1 depuis la case n+1, soit un bond de 2 depuis la case n...

par **cocmarseillais** » 19 Mai 2009, 16:19

maturin a écrit:Ben pour arriver sur la dernière case n+2 elle fait soit un bond de 1 depuis la case n+1, soit un bond de 2 depuis la case n...

merci de ta réponse je pense que cela suffira

merci bonne soirée

par **cocmarseillais** » 21 Mai 2009, 10:59

Bonjour,

dans la suite de ce dm j'ai encore rencontré des difficulté:

je doit montrer que pour tout réels X et Y on a Un= X*q^n + Y*q'^n

avec q et q' les solutions de l'équation caractéristiques de la suites de Fibonacci.

Pouvez vous m'aider ??

merci

par **Zweig** » 21 Mai 2009, 11:31

Salut,

(c'est plutôt un problème de Supérieur ça, "équation caractéristique", 'fin bon)

L'équation caractéristique associée à la suite de Fibonacci est :

Les deux solutions sont

et

.

Tu pose

et montre que

, en n'oubliant pas que

, pareil pour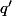

.

J'anticipe la suite de l'exercice. Tu vas devoir certainement déterminer

et

. Pour cela, résous le système :

Vois pourquoi.

par **cocmarseillais** » 21 Mai 2009, 20:09

merci beaucoup mais comment établir la relation entre Un= X*q^n + Y*q'^n et Un+2-Un+1-Un= 0 ?

par **Ericovitchi** » 22 Mai 2009, 09:13

il y a un topic recent qui traitait aussi la question :
lien

Suite de Fibonacci

Suite de Fibonacci

Qui est en ligne