Suite de fibonacci

[flo314]

bonjour,j'ai les suites géométriques définies par Un+2 = Un+1 + Un et de 1er terme 1.J'ai trouvé leur raisons qui sont q = (1+racine5)/2 et q' = (1-racine5)/2
je dois maintenant démontrer que pour tous réels A et B : Un = A.q^n + B.q'^n verifie l'équation Un+2 = Un+1 + Un.J'ai essayer quelque truc mai sans résultat si quelqu'un pourrait m'aider svp.

[Ericovitchi]

Tu pars de Un+2 et tu utilises le fait que
et que (idem pour q') et tu vas trouver facilement Un+1+Un

[flo314]

ok j'ai essayé et j'arrive à Un+2 = A.q^n+1 + A.q^n + B.q'^n+1 + B.q'^n c'est sa ? et je fais quoi avec sa je peux dire que c'est égale a Un+1 + Un puisque Un = A.q^n + B.q'^n ?

[maturin]

oui et tu mets un peu en facteur pour faire apparaitre l'expression de ericovitchi
tu dis Un+2=A(1+q)q^n+B(1+q')q'^n

et l'hypothèse de ta récurrence c'est que Un=Aq^n+Bq'^n est vrai pour n et n+1.

Il te reste à le montre pour u0 et u1 ce qui va te contraindre tes A et B.

[flo314]

ok mais pour U0 je trouve A+B=1 et apres pour U1 j'ai Aq + Bq' =1 car la suite est definie par U0 = 1 et U1 = 1 j'ai donc remplacer Aq+Bq' par (1-B)q+Bq' mais je tombe sur des résultats pour A et B qui ne colle pas avec la question 3 de mon dm

[Ericovitchi]

non il faut carrément résoudre le système
A+B=1
Aq + Bq' =1

tu multiplies la première par q et tu soustrais
(et tu te rappelles que ) et tu trouves A et B

[flo314]

ha ok d accord je trouve B = 1/racine(5) et A = (racine(5)-1)/racine(5)

[Ericovitchi]

pas sûr ça, je ne vois pas bien comment tu trouves ça
ton résultat ne respecte pas la symétrie naturelle qu'il y a entre A et B

Bq-Bq'=q-1 -->

[flo314]

je trouve B = (racine(5)-1)/(2racine(5)) :look_up:

[Ericovitchi]

oui, c'est la même chose que ce que j'ai affiché, il suffit de simplifier

[flo314]

ok c'est bon je suis vraiment con j'ai bien trouver pareil.
Par contre je doit en déduire que Un= (q^(n+1)-q'^(n+1))/racine(5)).J'ai essayer en remplaçant q^n+1 et q'^n+1 par la formule précédente mais je n'arrive pas à avoir Un en fonction de Un+1.En fait je vois pas comment définir un terme en fonction du suivant.

[Ericovitchi]

curieux ce que tu as à démontrer, tu es sûr ?
Pour moi Alors pour trouver à partir de ça, il y a quelque chose qui a dû m'échapper :triste:

[flo314]

ba pourtant c'est bien sa la question je vois pas du tout comment faire

[flo314]

bon j ai trouvé Un = (q^n+1 + q'^n+1)/rac(5) mais pas Un = (q^n+1 - q'^n+1)/rac(5)

[busard_des_roseaux]

re,

l'idée c'est

si

alors quelque soit n,


soit


les coordonnées (a,b) des deux premiers termes et sont les coordonnées de la suite
par rapport au repère de base et


on a donc un isomorphisme entre cet ensemble de suites qui récurrent
et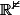

En règle générale, quand on étudie une suite définie par récurrence,
on se demande comment cette suite dépend de son (ou de ses) premiers termes:
de manière linéaire, continue, de manière différentiable,etc..

[flo314]

oula j'ai rien compris busard sa doit pas etre du niveau 1er s

[busard_des_roseaux]

oula j'ai rien compris busard sa doit pas etre du niveau 1er s

j'ai écrit des fléches sur les suites pour que tu voies l'analogie avec les
coordonnées des vecteurs :zen:

[flo314]

bon c'est bon j'ai réussit à montrer que Un = (q^n+1 - q'^n+1)/rac(5).

[flo314]

il me reste plus qu'a trouver la limite de Un+1/Un.Sa doit être le nombre d'or non ?

[Zweig]

Exact ! Même, plus généralement, pour tout entier naturel fixé, et si on note le nombre d'or, alors :