Suite algorithme fibonacci

[maeganna]

Bonjour, :help:
Nous devons faire un DM sur la suite de Fibonacci avec des lapins ci-dessous. Nous avons réussi les deux premières questions (1 et 2). En revanche la question 3 nous est incompréhensible. Nous avons du mal à comprendre comment fonctionne l'algorithme demandé car il faut utiliser la "valeur d'or". Pouvez-vous nous aider? Nous avons trouver pour la question 2 deux formules: Fn=(Fn-1)+(Fn-2) et Fn+2=(Fn+1)+Fn. En contactant notre professeur, il nous a indiquer que w est une variable tampon de u. Merci d'avance!

Énoncé:

On place dans un enclos un couple de lapereaux. Chaque couple âgé de deux mois donne naissance à un nouveau couple. Si aucun lapin ne meurt, combien y aura t-il de couples le n-ième mois?
On note Fn le nombre de couples de lapins le n-ième mois; on a donc F1=1
1) a) Justifier que F2=1, F3=2 et F4=3
b) Calculer F5 et F6
2. Soit n supérieur à 1, exprimer Fn+2 en fonction de Fn et Fn+1
3.a. Recopier et compléter l'algorithme ci-dessous pour que l'affichage obtenu en entrant un entier naturel k corresponde à Fk :

Variables
k,n ; entiers
u,v,w ; réels
Traitement
Demander k
n prend la valeur 1
u prend la valeur 1
v prend la valeur 1
tant que n ...
w prend la valeur ...
u prend la valeur ...
v prend la valeur ...
n prend la valeur ...
fin tant que
Sortie
Afficher u

b. Programmer cet algorithme
c. Quel est le nombre de couples de lapins au bout d'un an ? de deux ans ?



Info: Léonard de Pise souvent appelé Fibonacci a donné son nom à une suite d'entier. Cette suite possède des propriétés intéressantes. En calculant le quotient de deux nombres consécutifs dans la suite de Fibonacci, on obtient une suite convergeant vers le nombre d'or.
;)=1+5/2

[Ben314]

Salut,
Concernant l'algorithme, il faut bien comprendre qu'une variable informatique, c'est une "case" qui contient à un moment donné une certaine valeur.

Dans ta boucle, à un moment donné, la variable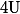 va contenir un certain terme de la suite et la variable 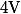va contenir .
A l'étape suivante de la boucle, tu voudrait que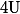 contienne et que 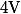contienne .
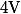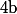Cela signifie que, partant de contient et contient on veut trouver une suite d'instruction permettant d'arriver à contient et 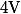contient

Le premier truc qui vient à l'esprit est de taper :
(1) U prend la valeur de V
(2) V prend la valeur de U+V
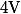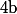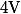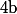Sauf que, partant de contient et contient , l'instruction (1) donne contient et contient puis l'instruction (2) donne contient et 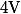contient : c'est pas bon...

Le deuxième truc qui vient à l'esprit est de taper :
(1) V prend la valeur de U+V
(2) U prend la valeur de V
Sauf que, partant de contient et 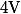contient , l'instruction (1) donne contient et 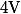contient puis l'instruction (2) donne contient et 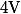contient : c'est toujours pas bon...

Ce qu'il faut comprendre, c'est qu'en exécutant l'instruction X prend la valeur de ... on perd la valeur qu'il y avait dans X vu qu'elle est remplacée par autre chose. L'idée est donc de la mémoriser dans une autre variable pour pouvoir la réutiliser ensuite.
En utilisant une 3em variable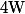 on peut par exemple faire :
Départ : contient , 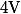contient 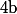, 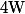contient
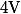(1) W prend la valeur de U contient , contient 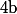, 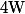contient
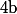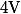(2) U prend la valeur de V contient , contient 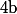, 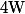contient
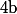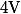(3) V prend la valeur de W+V contient , contient , 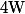contient

Il y a pas mal d'autres solutions en utilisant une "variable temporaire" W, et si on est très malin, on arrive même à trouver des solutions SANS utiliser de variables temporaires, par exemple :
Départ : contient , 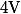contient
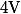(1) V prend la valeur de U+V contient , contient
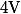(2) U prend la valeur de V-U contient , contient

En informatique, le cas archi classique où on utilise une "variable temporaire" est celui où on veut échanger la valeur de deux variables, c'est à dire, partant de contient , 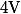contient on veut arriver à contient 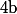, 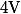contient . La solution "classique" est de taper :
(1) W prend la valeur de U
(2) U prend la valeur de V
(3) V prend la valeur de W