Bonjour, j'espère que vous allez bien.
pourriez- vous m'aider concernant la dernière question de cet exo ?
https://zupimages.net/viewer.php?id=23/21/iuo8.png
Pour la 4-a, j'ai distingué 2 cas, selon la parité de n
Pour la dernière, j'ai appliqué la formule du binôme et divisé le sigma en 2, (pairs/impairs) et j'ai remplacé D^k par l'expression trouvée dans 4-a mais je n'arrive pas à conclure.
Merci d'avance
Structures algébriques
11 messages
- Page 1 sur 1
Re: Structures algébriques
par Ben314 » 28 Mai 2023, 18:12
Salut,
Je peut commencer par une "vague indication" pour voir si ça te suffit.
Quand tu as un polynôme P(X), pour obtenir un nouveau polynôme contenant uniquement les termes de degrés pairs (ou uniquement impairs) de P, on peut songer à ajouter/retrancher P(X) et P(-X).
Par exemple, partant de^7)
on peut trouver une écriture assez simple 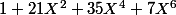de 
et de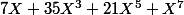 
Je peut commencer par une "vague indication" pour voir si ça te suffit.
Quand tu as un polynôme P(X), pour obtenir un nouveau polynôme contenant uniquement les termes de degrés pairs (ou uniquement impairs) de P, on peut songer à ajouter/retrancher P(X) et P(-X).
Par exemple, partant de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Structures algébriques
par Arc » 28 Mai 2023, 18:44
Salut,
j'ai effectué quelques essais, mais la situation ne se débloque pas ...
j'ai effectué quelques essais, mais la situation ne se débloque pas ...
Re: Structures algébriques
par Ben314 » 28 Mai 2023, 19:05
Normalement, tu devrait trouver un (ou plutôt deux) trucs de ce style :
)
Somme pour 
pair entre 
et 
de ^{k/2})
où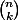
désigne le coefficient binomial.
S'il y avait pas le "pour pair", la valeur du bidule découlerais immédiatament de la formile du binôme de Newton modulo la petite astuce consistant à écrire que ^{k/2}=\big(i\sqrt{3}\big)^k)
.
Et l'indic. que je te donne, c'est pour voir comment, partant de la formule du binôme de Newton^n)
en déduire les valeurs 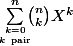de 
et de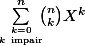 
qui sont les formules dont tu as besoin pour simplifier
où
S'il y avait pas le "pour
Et l'indic. que je te donne, c'est pour voir comment, partant de la formule du binôme de Newton
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Structures algébriques
par Arc » 29 Mai 2023, 13:16
Bonjour,
oui je suis bien parvenu à cette étape, mais même avec votre indication, je ne parviens pas à expliciter la puissance en fonction de n
oui je suis bien parvenu à cette étape, mais même avec votre indication, je ne parviens pas à expliciter la puissance en fonction de n
Re: Structures algébriques
par Ben314 » 29 Mai 2023, 13:31
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Structures algébriques
par Arc » 29 Mai 2023, 13:44
cela revient à écrire (1+X)^n = [( (1+X)^n+ (1-X)^n)/2]+[((1+X)^n- (1-X)^n)/2]
est-ce notre objectif ?
est-ce notre objectif ?
Re: Structures algébriques
par Ben314 » 29 Mai 2023, 14:14
Bon, on va pas y passer la nuit non plus . . .
Du fait que^k\!=\!X^k)
pour pair et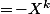 
pour impair on a
^n=\big(1\!+\!(-X)\big)^{\!n}=\sum_{k=0}^n\!\binom{n}{k}(-X)^k=\sum_{{k=0}\atop{k \ \text{pair}}}^n\!\!\!\!\binom{n}{k}X^k-\!\!\!\!\!\!\sum_{{k=0}\atop{k \ \text{impair}}}^n\!\!\!\!\!\!\binom{n}{k}X^k)
Et, bien sûr, on a aussi
^n=\sum_{k=0}^n\!\binom{n}{k}X^k=\sum_{{k=0}\atop{k \ \text{pair}}}^n\!\!\!\!\binom{n}{k}X^k+\!\!\!\!\!\!\sum_{{k=0}\atop{k \ \text{impair}}}^n\!\!\!\!\!\!\binom{n}{k}X^k)
Et, en ajoutant/soutrayant, on en déduit que :
\ \ \ \sum_{{k=0}\atop{k \ \text{pair}}}^n\!\!\!\!\binom{n}{k}X^k=\frac{1}{2}\Big((1\!+\!X)^n\!+(1\!-\!X)^n\Big)\ \ \ ;\ \ \ \sum_{{k=0}\atop{k \ \text{impair}}}^n\!\!\!\!\!\!\binom{n}{k}X^k=\frac{1}{2}\Big((1\!+\!X)^n\!-(1\!-\!X)^n\Big))
Ensuite, normalement, tu as du trouver que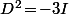
ce qui implique que ^{k/2}I)
pour pair et ^{(k-1)/2}D)
pour impair.
Puis, du fait que les matrices
et 
commutent (attention à bien le préciser vu que, sinon, la formule du binôme de Newton serait fausse) on a :
^n=\sum_{k=0}^n\!\binom{n}{k}D^k=\alpha I+\beta D\ \ \text{o\`u}\ \ \ \alpha\!=\!\!\!\sum_{{k=0}\atop{k \ \text{pair}}}^n\!\!\!\!\binom{n}{k}(-3)^{k/2}\ \ \ \text{et}\ \ \ \beta\!=\!\!\!\!\!\!\sum_{{k=0}\atop{k \ \text{impair}}}^n\!\!\!\!\!\!\binom{n}{k}(-3)^{(k-1)/2})
Et on utilise les formules avec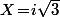 
(pour avoir 
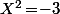) pour exprimer plus simplement les valeurs des coefficients 
et 
.
Du fait que
Et, bien sûr, on a aussi
Et, en ajoutant/soutrayant, on en déduit que :
Ensuite, normalement, tu as du trouver que
Puis, du fait que les matrices
Et on utilise les formules
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Structures algébriques
par GaBuZoMeu » 29 Mai 2023, 14:37
Bonjour,
L'objectif de la question 4 n'est pas formulé très clairement. On peut penser qu'il s'agit d'exprimer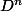
et ^n)
sous la forme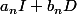 
.
Dans ce cas, il est bien plus simple d'avoir des formules dépendant de la parité de pour 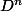et de la classe de modulo 3 pour .
La machinerie derrière l'exercice s'éclaire quand on réalise que le corps
est isomorphe à 
par un isomorphisme qui envoie sur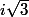 
, et donc 
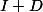sur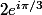 
.
L'objectif de la question 4 n'est pas formulé très clairement. On peut penser qu'il s'agit d'exprimer
Dans ce cas, il est bien plus simple d'avoir des formules dépendant de la parité de
La machinerie derrière l'exercice s'éclaire quand on réalise que le corps
Re: Structures algébriques
par GaBuZoMeu » 29 Mai 2023, 14:38
Au fait, tu t'es visiblement trompé de section de forum : ce n'est clairement pas "Lycée".
Re: Structures algébriques
par Arc » 29 Mai 2023, 15:01
Bonjour, je vous remercie pour vos réponses et vos éclaircissements.
Il s'agit bien du lycée, mais du programme marocain (terminale filière science maths uniquement).
Il s'agit bien du lycée, mais du programme marocain (terminale filière science maths uniquement).
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :