Bonjour
Je vais utiliser une propriété qui n'est pas expressément au programme de lycée mais que vous avez plus ou moins recontrée.
Soit le système
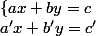
On appelle déterminant du système le nombre D=ab'-a'b.
Si D est non nul alors le système admet une solution unique.
Si D=0 alors les 2 équations sont soient incompatibles soit équivalentes.
J'en viens au problème.
Puisque |a|=1 , je pose
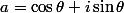
et
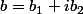
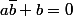
équivaut à :
(b_1-ib_2)+b_1+ib_2=0)
+i(b_1\sin \theta-b_2\cos \theta +b_2)=0)
On a donc le système d'inconnues b1 et b2 :
+b_2\sin \theta =0 \\ b_1\sin \theta +b_2(1-\cos \theta)=0 \right)
Le déterminant du système est égal à
(1-\cos \theta)-\sin^2 \theta=1-\cos^2 \theta-\sin^2 \theta=0)
Le système admet une solution évidente
0,0) donc les deux équations sont équivalentes. La relation liant a et b est donc traduite par l'une ou l'autre des deux égalités du système.
Une similitude indirecte a pour expression complexe
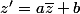
. Cherchons les points fixes en posant z=x+iy
x+iy=a(x-iy)+b
(x-iy)=b_1+ib_2)
+i(y+y\cos \theta-x\sin \theta)=b_1+ib_2)
x et y sont donc solutions du système :
-y\sin \theta=b_1 \\ -x\sin \theta +y(1+\cos \theta)=b_2 \right)
Le déterminant du système est égal à
Multiplions la première équation par
et la seconde par
+y\sin^2 \theta =-b_1 \sin \theta \\ -x\sin \theta (1-\cos \theta) +y(1-\cos^2 \theta) =b_2(1-\cos \theta )\right)
Les coefficients respectifs de x et y sont les mêmes dans les deux équations et on a vu précédemment que
=0)
. Les deux équations sont donc équivalentes.
x et y sont donc liés par exemple par la relation :
-y\sin \theta=b_1)
qui est l'équation d'une droite.
La similtude indirecte est une isométrie puisque |a|=1 qui a une droite de points fixes, c'est donc une symétrie axiale.
Remarque : avec les deux relations données sur a et b il est aussi possible d'obtenir des similitudes directes.
